Question

已知曲线C：y=

-x2-2x

与直线l：x+y-m=0有两个交点，则m的取值范围是

 

．

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

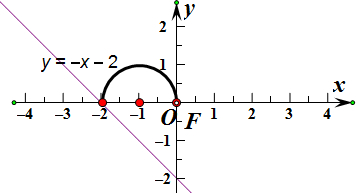
分析：先将直线与曲线化简，做出图象，然后利用图象找出符合题意的直线的位置，一条过（-2，0），一条与半圆弧相切，求出对应的m值，得出答案．

解答： 解：曲线C：y=

-x2-2x

化简为（x+1）²+y²=1（y≥0），是以（-1，0）为圆心，1为半径的半圆弧，
直线l：x+y-m=0，化为斜截式；y=-x+m，斜率为-1的直线，m为直线在y轴上的截距，
有图象可知，当直线过（-2，0）时，与半圆相交，且在y轴上截距为-2，故m≥-2，
将直线方程代入圆的方程得（x+1）²+（-x+m）²=1，化简得2x²+2（1-m）x+m²=0，
当直线与圆相切时，由△=m²+2m-1=0，解得m=-1-

2

（舍去），或m=-1+

2

，
综上，m的取值范围是-2≤m≤-1+

2

．
故答案为：[-1，-1+

2

]．

点评：本题考察直线与圆的位置关系，解题关键为对曲线方程的化简，y≥0的立即，得出曲线为半圆弧．