题目内容
已知实数x,y满足
.
求下列目标函数的取值范围.
(1)z1=2x-y
(2)z1=
.
|
求下列目标函数的取值范围.
(1)z1=2x-y
(2)z1=
| y+5 |
| x+5 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
解答:
解:出不等式组对应的平面区域如图: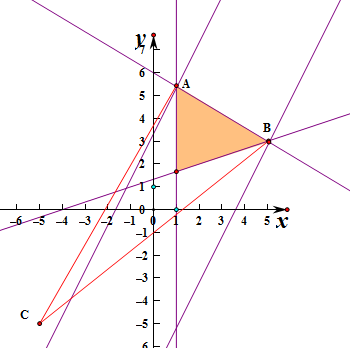
(1)由z=2x-y得y=2x-z,
平移直线y=2x-z,
由图象可知当直线y=2x-z经过点B时,直线y=2x-z的截距最小,
此时z最大.
由
,解得
,即B(5,3)
将B(5,3)的坐标代入目标函数z=2x-y,
得z=10-3=7.即z=2x-y的最大值为7.
当直线y=2x-z经过点a时,直线y=2x-z的截距最大,
此时z最小.
由
,解得
,即A(1,
),此时z=2x-y=2-
=-
,
即-
≤z≤7.
(2)求z=
的几何意义是到点C(-5,-5)的斜率,
由图象可知AC的斜率最大为
=
,BC的斜率最小为
=
,
即
≤z≤
.

(1)由z=2x-y得y=2x-z,
平移直线y=2x-z,
由图象可知当直线y=2x-z经过点B时,直线y=2x-z的截距最小,
此时z最大.
由
|
|
将B(5,3)的坐标代入目标函数z=2x-y,
得z=10-3=7.即z=2x-y的最大值为7.
当直线y=2x-z经过点a时,直线y=2x-z的截距最大,
此时z最小.
由
|
|
| 27 |
| 5 |
| 27 |
| 5 |
| 17 |
| 5 |
即-
| 17 |
| 5 |
(2)求z=
| y+5 |
| x+5 |
由图象可知AC的斜率最大为
| ||
| 1+5 |
| 26 |
| 15 |
| 3+5 |
| 5+5 |
| 4 |
| 5 |
即
| 4 |
| 5 |
| 26 |
| 16 |
点评:本题主要考查线性规划的应用,利用z的几何意义是解决本题的关键,注意使用数形结合.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
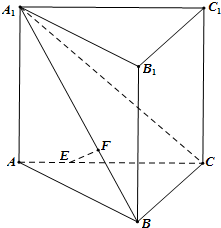 如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.
如图,在直三棱柱ABC-A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.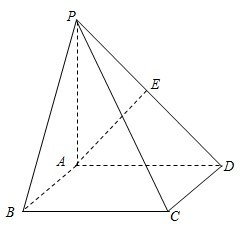 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD,E为PD中点.