题目内容
已知数列{an},其前n项和为Sn,满足2Sn=3an-3(n∈N*)数列{
}是等差数列,其第三项和第九项分别是a1和-a2
(1)求数列{an}的通项公式an;
(2)求数列{cn}的通项公式及前n项和Tn;
(3)如果对任意的n∈N*,不等式-t2+at+80≥cn恒成立,求使关于t的不等式有解的充要条件.
| cn |
| an |
(1)求数列{an}的通项公式an;
(2)求数列{cn}的通项公式及前n项和Tn;
(3)如果对任意的n∈N*,不等式-t2+at+80≥cn恒成立,求使关于t的不等式有解的充要条件.
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)利用递推式的意义、等比数列的通项公式即可得出;
(2)利用等差数列的通项公式与“错位相减法”、等比数列的前n项和公式即可得出;
(3)对任意的n∈N*,不等式-t2+at+80≥cn恒成立?不等式-t2+at+80≥(cn)max.由cn=(9-2n)×3n.可得(cn)max=c3=c4=81.-t2+at+80≥81化为t2-at+1≤0有解的充要条件△≥0,解出即可.
(2)利用等差数列的通项公式与“错位相减法”、等比数列的前n项和公式即可得出;
(3)对任意的n∈N*,不等式-t2+at+80≥cn恒成立?不等式-t2+at+80≥(cn)max.由cn=(9-2n)×3n.可得(cn)max=c3=c4=81.-t2+at+80≥81化为t2-at+1≤0有解的充要条件△≥0,解出即可.
解答:
解:(1)∵2Sn=3an-3,∴当n≥2时,2Sn-1=3an-1-3,
∴2an=2Sn-2Sn-1=3an-3-(3an-1-3),化为an=3an-1.
当n=1时,2a1=2S1=3a1-3,解得a1=3.
∴sl{an}是等比数列,
an=3×3n-1=3n.
(2)∵数列{
}是等差数列,其第三项和第九项分别是a1和-a2,设公差为d.
∴
=3,
=-9,
∴-9=3+6d,解得d=-2.
∴
=3-2(n-3)=9-2n,
∴cn=(9-2n)×3n.
∴Tn=7×3+5×32+3×33+…+(11-2n)×3n-1+(9-2n)×3n,
3Tn=7×32+5×33+…+(11-2n)×3n+(9-2n)×3n+1,
∴-2Tn=7×3-2×32-2×33-…-2×3n-(9-2n)×3n+1=27-
-(9-2n)×3n+1=30-(10-2n)×3n+1,
∴Tn=(5-n)×3n+1-15.
(3)对任意的n∈N*,不等式-t2+at+80≥cn恒成立?不等式-t2+at+80≥(cn)max,
∵cn=(9-2n)×3n.c1=21,c2=45,c3=81,c4=81,当n≥5时,c5<0,
∴(cn)max=c3=c4=81.
∴-t2+at+80≥81,
∴t2-at+1≤0有解的充要条件△≥0,
∴△=a2-4≥0,
解得a≥2或a≤-2.
∴关于t的不等式有解的充要条件是a≥2或a≤-2.
∴2an=2Sn-2Sn-1=3an-3-(3an-1-3),化为an=3an-1.
当n=1时,2a1=2S1=3a1-3,解得a1=3.
∴sl{an}是等比数列,
an=3×3n-1=3n.
(2)∵数列{
| cn |
| an |
∴
| c3 |
| a3 |
| c9 |
| a9 |
∴-9=3+6d,解得d=-2.
∴
| cn |
| an |
∴cn=(9-2n)×3n.
∴Tn=7×3+5×32+3×33+…+(11-2n)×3n-1+(9-2n)×3n,
3Tn=7×32+5×33+…+(11-2n)×3n+(9-2n)×3n+1,
∴-2Tn=7×3-2×32-2×33-…-2×3n-(9-2n)×3n+1=27-
| 2×3(3n-1) |
| 3-1 |
∴Tn=(5-n)×3n+1-15.
(3)对任意的n∈N*,不等式-t2+at+80≥cn恒成立?不等式-t2+at+80≥(cn)max,
∵cn=(9-2n)×3n.c1=21,c2=45,c3=81,c4=81,当n≥5时,c5<0,
∴(cn)max=c3=c4=81.
∴-t2+at+80≥81,
∴t2-at+1≤0有解的充要条件△≥0,
∴△=a2-4≥0,
解得a≥2或a≤-2.
∴关于t的不等式有解的充要条件是a≥2或a≤-2.
点评:本题考查了递推式的应用、等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”、一元二次不等式的解集与判别式的关系,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
在区间(a,b)上函数f(x),g(x)都是增函数,则F(x)=f(x)g(x)在(a,b)上( )
| A、增函数 | B、减函数 |
| C、增函数或减函数 | D、以上都不对 |
函数y=
在定义域内是( )
| lgcosx |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
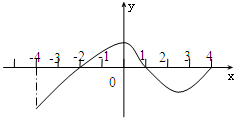
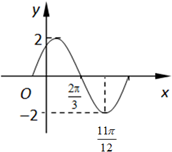 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.