题目内容
下列命题:
①△ABC的三边分别为a,b,c则该三角形是等边三角形的充要条件为a2+b2+c2=ab+ac+bc;
②在△ABC中,“A>B”是“sinA>sinB”的充要条件;
③若命题P:?x∈R,tanx=1;命题q:?x∈R,x2-x+1>0,则命题“p且-q“是假命题;
④已知a1,b1,c1,a2,b2,c2都是不等于零的实数,关于x的不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为P,Q,则
=
=
是P=Q的充分必要条件;
⑤“函数f(x)=tan(x+ϕ)为奇函数”的充要条件是“ϕ=kπ(k∈Z)”.
其中正确的命题是 .
①△ABC的三边分别为a,b,c则该三角形是等边三角形的充要条件为a2+b2+c2=ab+ac+bc;
②在△ABC中,“A>B”是“sinA>sinB”的充要条件;
③若命题P:?x∈R,tanx=1;命题q:?x∈R,x2-x+1>0,则命题“p且-q“是假命题;
④已知a1,b1,c1,a2,b2,c2都是不等于零的实数,关于x的不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为P,Q,则
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
⑤“函数f(x)=tan(x+ϕ)为奇函数”的充要条件是“ϕ=kπ(k∈Z)”.
其中正确的命题是
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①:显然a=b=c能推出右边,从右推左边时,应将式子适当变形,能够得到三数相等;
对于②:结合三角形内角的范围及内角和定理以及正弦函数的单调性可以判断;
对于③:分别判断两个简单命题的真假,进而根据复合命题真假判断的真值表,可得结论;
对于④:举个反例即可说明必要性不成立.
对于⑤:结合正切函数的图象和性质,可以判断.
对于②:结合三角形内角的范围及内角和定理以及正弦函数的单调性可以判断;
对于③:分别判断两个简单命题的真假,进而根据复合命题真假判断的真值表,可得结论;
对于④:举个反例即可说明必要性不成立.
对于⑤:结合正切函数的图象和性质,可以判断.
解答:
解:对于①:显然必要性成立,反之若a2+b2+c2=ab+ac+bc,则2(a2+b2+c2)=2(ab+ac+bc),整理得(a-b)2+(a-c)2+(b-c)2=0,当且仅当a=b=c时成立故充分性成立,故①是真命题;
对于②:在三角形中,“A>B”?“a>b“?“2RsinA>2RsinB“?“sinA>sinB”,故②是真命题;
对于③:命题P:?x∈R,tanx=1为真,;命题q:?x∈R,x2-x+1>0为真,则命题“p且-q“是假命题,故③是真命题;
对于④:实际上不等式x2+x+5>0与x2+x+2>0的解集都是R,但是
=
≠
,故不满足必要性,故④是假命题.
对于⑤:“函数f(x)=tan(x+ϕ)为奇函数”的充要条件是“ϕ=
kπ(k∈Z)”,故⑤是假命题.
故正确的命题有:①②③,
故答案为:①②③.
对于②:在三角形中,“A>B”?“a>b“?“2RsinA>2RsinB“?“sinA>sinB”,故②是真命题;
对于③:命题P:?x∈R,tanx=1为真,;命题q:?x∈R,x2-x+1>0为真,则命题“p且-q“是假命题,故③是真命题;
对于④:实际上不等式x2+x+5>0与x2+x+2>0的解集都是R,但是
| 1 |
| 1 |
| 1 |
| 1 |
| 5 |
| 2 |
对于⑤:“函数f(x)=tan(x+ϕ)为奇函数”的充要条件是“ϕ=
| 1 |
| 2 |
故正确的命题有:①②③,
故答案为:①②③.
点评:本题是简易逻辑与其它知识的综合考查,实际上已命题真假的判断方法为手段考查相关的基础知识,前提是必须熟练准确理解基本概念,掌握基本方法.

练习册系列答案
相关题目
函数y=
在定义域内是( )
| lgcosx |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
设I是函数y=f(x)的定义域,若存在x0∈I,使f(x0)=-x0,则称x0是f(x)的一个“次不动点”,也称f(x)在区间I上存在“次不动点”.若函数f(x)=ax3-3x2-x+1在R上存在三个“次不动点x0”,则实数a的取值范围是( )
| A、(-2,0)∪(0,2) |
| B、(-2,2) |
| C、(-1,0)∪(0,1) |
| D、(-1,1) |
执行如图所示的程序框图,若f(x)=3x2-1,取?=
,则输出的值为( )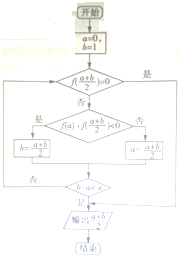
| 1 |
| 10 |

A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
,
,其中
=(-1,
),且
⊥(
-3
),则
在
上的投影为 ( )
| a |
| b |
| a |
| 3 |
| a |
| a |
| b |
| b |
| a |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若0<m<1,0<n<1,则
的最大值为( )
| mn(1-m-n) |
| (m+n)(1-m)(1-n) |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
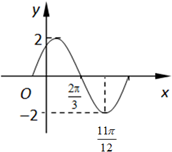 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.