题目内容

3．设命题p：?x＞0，sinx＞2x-1，则￢p为（　　）
A．?x＞0，sinx≤2x-1B．?x＞0，sinx＜2x-1C．?x＞0，sinx＜2x-1D．?x＞0，sinx≤2x-1

分析 直接利用特称命题的否定是全称命题写出结果即可．

解答 解：命题p：?x＞0，sinx＞2x-1，
则￢p为：?x＞0，sinx≤2x-1，
故选：A．

点评 本题考查特称命题与全称命题的否定关系，基本知识的考查．

练习册系列答案
相关题目
13．已知集合A={0，a，a2}，且1∈A，则a=（　　）
A．1B．-1C．±1D．0
14．等差数列{an}中，a1+a7=8，则a2+a4+a6=（　　）
A．8B．12C．16D．20
11．若曲线y=kx2+lnx在点（1，k）处的切线与直线2x-y+3=0平行，则k=$\frac{1}{2}$．
18．如图是一个算法的程序框图，当输入x的值为3时，输出y的结果恰好是$\frac{1}{3}$，则？处的关系式可以是（　　）
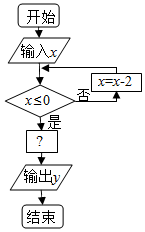
A．y=x2B．y=3-xC．y=3xD．y=x${\;}^{\frac{1}{3}}$
8．已知数列{an}的前n项和Sn满足2an+1-Sn=0，且a1=1．
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）求数列{nan}的前n项和Tn．
15．已知定义在（0，+∞）上的单调函数f（x），对任意的x∈（0，+∞），都有f[f（x）-log3x]=4，则函数f（x）的图象在x=$\frac{1}{ln3}$处的切线的斜率为1．
12．集合A={x|x≤a}，B={x|x2-5x＜0}，若A∩B=B，则a的取值范围是（　　）
A．a≥5B．a≥4C．a＜5D．a＜4
13．已知数列{an}的首项a1=a，其前n项和为Sn，且满足Sn+Sn-1=3n2+2n+4（n≥2），若对任意的n∈N*，an＜an+1恒成立，则a的取值范围是（　　）
A．（$\frac{23}{4}$，$\frac{29}{4}$）B．（$\frac{20}{3}$，$\frac{29}{4}$）C．（$\frac{23}{4}$，$\frac{20}{3}$）D．（-∞，$\frac{20}{3}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网