题目内容
在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,如果c=
a,∠B=45°,那么∠C等于( )
| 2 |
| A、120° | B、105° |
| C、90° | D、75° |
考点:余弦定理的应用
专题:计算题,解三角形
分析:先求出A+C=135°,再由正弦定理可得sinC=
sinA=
sin(150°-C),再由两角差的正弦公式化简即可得到cosC=0,从而求得C的值.
| 2 |
| 2 |
解答:
解:∵在△ABC中,∠B=45°,则A+C=135°,
∵c=
a,
∴sinC=
sinA=
sin(135°-C)=
(
cosC+
sinC)=cosC+sinC,
∴cosC=0,
∵0°<C<180°,
∴C=90°
故选:C.
∵c=
| 2 |
∴sinC=
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴cosC=0,
∵0°<C<180°,
∴C=90°
故选:C.
点评:本题主要考查两角和的正弦公式,正弦定理以及同角三角函数的基本关系的应用,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
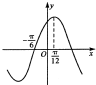 如图所示是函数f(x)=sin(?x+φ)(?>0,|φ|<π)的部分图象,则f(x)的解析式为
如图所示是函数f(x)=sin(?x+φ)(?>0,|φ|<π)的部分图象,则f(x)的解析式为