题目内容
5.在△ABC中,三边a,b,c的对角分别为A,B,C,若a2+b2=2018c2,则$\frac{2sinAsinBcosC}{{1-{{cos}^2}C}}$=2017.分析 利用余弦定理表示出cosC,把已知等式代入得到关系式,记作①,利用正弦定理化简,整理即可得出所求式子结果.
解答 解:在△ABC中,∵a2+b2=2018c2,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{2017{c}^{2}}{2ab}$,即2abcosC=2017c2,①
由正弦定理 $\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$=2R,得到a=2RsinA,b=2RsinB,c=2RsinC,
代入①得:2•2RsinA•2RsinBcosC=2017•4R2sin2C,即2sinAsinBcosC=2017sin2C=2017(1-cos2C),
则 $\frac{2sinAsinBcosC}{{1-{{cos}^2}C}}$=2017.
故答案为:2017.
点评 此题考查了余弦定理,正弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
15.已知集合$M=\left\{{x\left|{\frac{x-5}{x+1}≤0}\right.}\right\}$,N={-3,-1,1,3,5},则M∩N=( )
| A. | {-3,-1,1,3,5} | B. | {-1,1,3,5} | C. | {1,3,5} | D. | {-3,-1,1,3,} |
20.已知奇函数f(x)在[0,+∞)上是增函数,若f(lnx)<0,则( )
| A. | $\frac{1}{e}$<x<1或x>1 | B. | 1<x<e | C. | 0<x<e或x>e | D. | 0<x<1 |
15.设集合A={x|1<x<3},集合B={x|x2>4},则集合A∩B等于( )
| A. | {x|2<x<3} | B. | {x|x>1} | C. | {x|1<x<2} | D. | {x|x>2} |
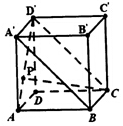
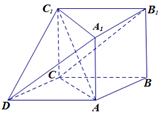 如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.
如图所示三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,AC⊥CD.