题目内容
9.已知点M(1,m)(m>1),若点N(x,y)在不等式组$\left\{\begin{array}{l}y≥x\\ y≤mx\\ x+y≤1\end{array}\right.$表示的平面区域内,且$\overrightarrow{OM}•\overrightarrow{ON}$(O为坐标原点)的最大值为2,则m=$1+\sqrt{2}$.
分析 利用向量的数量积化简表达式,得到目标函数,画出可行域,利用最优解求解即可.
解答 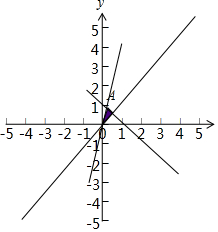 解:$1+\sqrt{2}$$\overrightarrow{OM}•\overrightarrow{ON}=x+my$,令x+my=z,
解:$1+\sqrt{2}$$\overrightarrow{OM}•\overrightarrow{ON}=x+my$,令x+my=z,
作出不等式组$\left\{\begin{array}{l}y≥x\\ y≤mx\\ x+y≤1\end{array}\right.$表示的可行域,由$\left\{\begin{array}{l}{y=mx}\\{x+y=1}\end{array}\right.$
解得A($\frac{1}{1+m}$,$\frac{m}{1+m}$),
当m≥0时,目标函数在A处取得最大值2.
分析知当$x=\frac{1}{1+m},y=\frac{m}{1+m}$时,zmax=2.
所以$\frac{1}{m+1}+m•\frac{m}{m+1}=2$,解之得$m=1+\sqrt{2}$或$m=1-\sqrt{2}$(舍去),
所以$m=1+\sqrt{2}$.
故答案为:$1+\sqrt{2}$.
点评 本题考查线性规划的简单应用,考查目标函数的最值的求法,值域可行域以及目标函数的最优解是解题的关键.

练习册系列答案
相关题目
20.已知奇函数f(x)在[0,+∞)上是增函数,若f(lnx)<0,则( )
| A. | $\frac{1}{e}$<x<1或x>1 | B. | 1<x<e | C. | 0<x<e或x>e | D. | 0<x<1 |
4.已知Tn为数列$\left\{{\frac{{{2^n}+1}}{2^n}}\right\}$的前n项和,若n>T10+1013恒成立,则整数n的最小值为( )
| A. | 1026 | B. | 1025 | C. | 1024 | D. | 1023 |
1.将编号为1,2,3,4,5,6的六个小球放入编号为1,2,3,4,5,6的六个盒子,每个盒子放一个小球,若有且只有三个盒子的编号与放入的小球编号相同,则不同的放法总数是( )
| A. | 40 | B. | 60 | C. | 80 | D. | 100 |
18.设n∈N*,则$\sqrt{\underbrace{11…1}_{2n个}-\underbrace{22…2}_{n个}}$=( )
| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{2n-1个}$ | C. | $\underbrace{33…3}_{{2^n}-1个}$ | D. | $\underbrace{33…3}_{2n个}$ |




