题目内容
5.已知f(x)=|x-3|.(I)证明:f(m)+f(-$\frac{1}{m}$)≥2;
(Ⅱ)若不等式f(x)+f(x+3)≥kx-1的解集为R,求实数k的取值范围.
分析 (I)f(m)+f(-$\frac{1}{m}$)=|m-3|+|3+$\frac{1}{m}$|,从而讨论去绝对值号,从而确定函数的单调性,从而证明;
(Ⅱ)由题意化简可得|x-3|+|x|≥kx-1的解集为R,作函数y=|x-3|+|x|与直线y=kx-1的图象,从而结合图象解得.
解答 解:(I)证明:f(m)+f(-$\frac{1}{m}$)
=|m-3|+|3+$\frac{1}{m}$|,
①当m≥3时,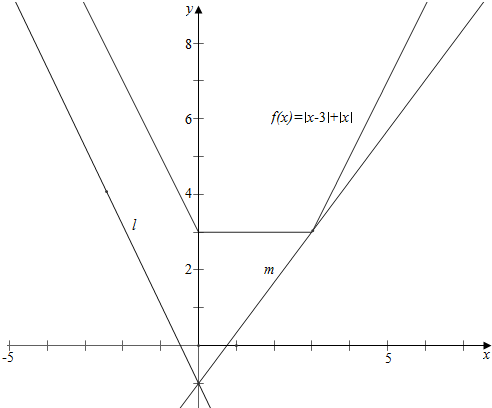
f(m)+f(-$\frac{1}{m}$)=m-3+3+$\frac{1}{m}$
=m+$\frac{1}{m}$≥$\frac{10}{3}$;
②当0<m<3时,
f(m)+f(-$\frac{1}{m}$)=3-m+3+$\frac{1}{m}$
=6-m+$\frac{1}{m}$>$\frac{10}{3}$;
③当-$\frac{1}{3}$<m<0时,
f(m)+f(-$\frac{1}{m}$)=3-m-3-$\frac{1}{m}$
=-m-$\frac{1}{m}$>$\frac{10}{3}$;
④当m≤-$\frac{1}{3}$时,
f(m)+f(-$\frac{1}{m}$)=3-m+3+$\frac{1}{m}$
=6-m+$\frac{1}{m}$≥$\frac{10}{3}$;
综上所述,f(m)+f(-$\frac{1}{m}$)≥2.
(Ⅱ)∵f(x)+f(x+3)≥kx-1的解集为R,
∴|x-3|+|x|≥kx-1的解集为R,
作函数y=|x-3|+|x|与直线y=kx-1的图象如图,
结合图象可知,
km=$\frac{3+1}{3}$=$\frac{4}{3}$,kl=-2,
故-2≤k≤$\frac{4}{3}$.
点评 本题考查了分类讨论与数形结合的思想应用及函数的单调性的判断与应用.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案| A. | α∥β | B. | α⊥β | ||
| C. | α与β相交但不垂直 | D. | 以上都不对 |
| A. | -$\frac{21}{8}$ | B. | $\frac{21}{8}$ | C. | -9 | D. | 9 |
| A. | {a,c,d,e} | B. | {a,c} | C. | {b,d} | D. | {d} |