题目内容
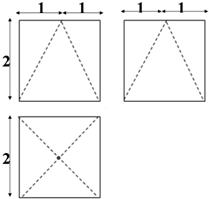
已知一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、8 | ||
B、
| ||
C、
| ||
| D、4 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图，可得该几何体是一个正方体挖去一个同底等高的四棱锥所得的组合体，代入棱柱和棱锥体积公式，相减可得答案．
解答：
解：由已知中的三视图，可得该几何体是一个正方体挖去一个同底等高的四棱锥所得的组合体，
正方体的体积为：2×2×2=8，
四棱锥的体积为：
×2×2×2=
，
故组合体的体积V=8-
=
，
故选：C
正方体的体积为：2×2×2=8，
四棱锥的体积为：
| 1 |
| 3 |
| 8 |
| 3 |
故组合体的体积V=8-
| 8 |
| 3 |
| 16 |
| 3 |
故选：C
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
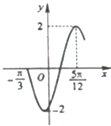
函数f（x）=2sin（ωx+φ）（ω＞0，-
＜φ＜
）的部分图象如图，则ω，φ的值分别是（ ）
| π |
| 2 |
| π |
| 2 |
A、ω=1，φ=-
| ||
B、ω=1，φ=-
| ||
C、ω=2，φ=-
| ||
D、ω=2，φ=-
|
为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：
下面的临界值供参考：
x2=
，其中n*1=n11+n22，n*2=n12+n21，n1*=n11+n12，n2*=n21+n22，n=n11+n22+n12+n21
下列结论正确的是（ ）
| 做不到“光盘” | 能做到“光盘” | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
x2=
| n(n11n22n12n21)2 |
| n1*n2*n*1n*2 |
| P（x2≥k） | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A、有95%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| B、有99%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| C、有99.5%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| D、性别不同决定了能否做到“光盘” |
设函数f（x）的导函数为f′（x），对任意x∈R都有0＜f′（x）＜2成立，则（ ）
| A、f（1）＜f（3）＜f（2）+2 |
| B、f（2）+2＜f（3）＜f（1） |
| C、f（1）＜f（2）+2＜f（3） |
| D、f（2）+2＜f（1）＜f（3） |
x为实数，[x]表示不超过x的最大整数（如[-1.5]=-2，[0]=0，[2.3]=2），则关于函数f（x）=x-[x]，x∈R的说法不正确的是（ ）
| A、函数不具有奇偶性 | ||||
| B、x∈[1，2）时函数是增函数 | ||||
| C、函数是周期函数 | ||||
D、若函数g（x）=f（x）-kx恰有两个零点，则k∈（-∞，-1）∪（
|
下列命题不正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
实数x，y满足
，则3x+y的最大值为（ ）
|
A、
| ||||||
B、3+
| ||||||
C、
| ||||||
| D、17 |
圆的标准方程为：（x-a-1）2+（y-b+2）2=r2其圆心坐标是（ ）
| A、（1，-2） |
| B、（-2，1） |
| C、（a+1，b-2） |
| D、（-a-1，-b+2） |