题目内容
圆锥的底面半径是1，它的侧面展开图是一个半圆，则它的母线长为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：半径为R的半圆卷成一个圆锥，则圆锥的母线长为R，底面半径r=
，进而可得答案．
| R |
| 2 |
解答：
解：半径为R的半圆卷成一个圆锥，
则圆锥的母线长为R，
设圆锥的底面半径为r，
则2πr=πR，
即r=
，
∵r=1，
∴R=2，
故答案为：2
则圆锥的母线长为R，
设圆锥的底面半径为r，
则2πr=πR，
即r=
| R |
| 2 |
∵r=1，
∴R=2，
故答案为：2
点评：本题考查旋转体，即圆锥的几何特征，分析出圆锥母线与底面半径的关系是解答的关键．
练习册系列答案
相关题目
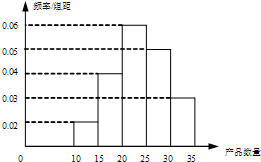为了调查某厂2000名工人生产某种产品的能力，随机抽查了m位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．已知生产的产品数量在[20，25）之间的工人有6位，则m=
复数a十bi（a，b∈R）的平方为实数的充要条件是（ ）
| A、a2+b2=0 |
| B、ab=0 |
| C、a=0，且b≠0 |
| D、a≠0，且b=0 |