题目内容
设函数f(x)=a-bsin(
-4x),其中a,b为实常数,x∈R,已知函数f(x)的值域是[1,5],求a,b的值.
| π |
| 3 |
考点:正弦函数的定义域和值域
专题:计算题,三角函数的图像与性质
分析:利用sin(
-4x)∈[-1,1],对b分b>0与b<0讨论,依题意,布列方程组,解之即可求得a,b的值.
| π |
| 3 |
解答:
解:∵f(x)=a-bsin(
-4x)的值域是[1,5],
∴当b>0时,有
,解得a=3,b=2;
当b<0时,有
,解得a=3,b=-2;
∴a=3,b=±2.
| π |
| 3 |
∴当b>0时,有
|
当b<0时,有
|
∴a=3,b=±2.
点评:本题考查正弦函数的定义域和值域,考查分类讨论思想与方程组思想,属于中档题.

练习册系列答案
相关题目
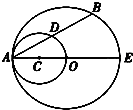 如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.
如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,求证:D是AB的中点.