题目内容
抛物线y2=4x的焦点到双曲线x2-
=1的渐近线的距离是 .
| y2 |
| 3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先确定抛物线的焦点位置,进而可确定抛物线的焦点坐标,再由题中条件求出双曲线的渐近线方程,再代入点到直线的距离公式即可求出结论.
解答:
解:抛物线y2=4x的焦点在x轴上,且p=2,
∴抛物线y2=4x的焦点坐标为(1,0),
由题得:双曲线x2-
=1的渐近线方程为x±
y=0,
∴F到其渐近线的距离d=
=
.
故答案为:
.
∴抛物线y2=4x的焦点坐标为(1,0),
由题得:双曲线x2-
| y2 |
| 3 |
| ||
| 3 |
∴F到其渐近线的距离d=
| 1 | ||||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查抛物线的性质,考查双曲线的基本性质,解题的关键是定型定位,属于基础题.

练习册系列答案
相关题目
设四个点P、A、B、C在同一球面上,且PA、PB、PC两两垂直,PA=3,PB=4,PC=5,那么这个球的表面积是( )
A、20
| ||
B、25
| ||
| C、25π | ||
| D、50π |

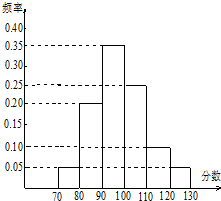 某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括
某校高三文科分为四个班.高三数学调研测试后,随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括