题目内容
18．若p=$\sqrt{a+2}$+$\sqrt{a+5}$，q=$\sqrt{a+3}$+$\sqrt{a+4}$，a≥0，则p、q的大小关系是（ ）| A． | p＜q | B． | p＞q | C． | p=q | D． | 由a的取值确定 |
分析 对P和q平方后作差即可得答案．
解答 解：∵p=$\sqrt{a+2}$+$\sqrt{a+5}$，
则p2=2a+7+2$\sqrt{（a+2）（a+5）}$
∵q=$\sqrt{a+3}$+$\sqrt{a+4}$，
则q2=2a+7+2$\sqrt{（a+3）（a+4）}$．
比较p，q的大小只需要比较（a+2）（a+5）与（a+3）（a+4）．
作差：（a+3）（a+4）-（a+2）（a+5）=12-10=2＞0
∴p＜q．
故选：A．
点评 本题考查了不等式的基本性质和比较大小，利用了作差法．属于基础题．
练习册系列答案
相关题目
9．
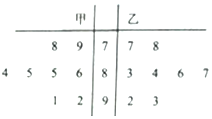甲、乙两名同学八次数学测试成绩如茎叶图所示，则甲同学成绩的众数与乙同学成绩的中位数依次为（ ）
甲、乙两名同学八次数学测试成绩如茎叶图所示，则甲同学成绩的众数与乙同学成绩的中位数依次为（ ）| A． | 85，86 | B． | 85，85 | C． | 86，85 | D． | 86，86 |
6．复数z1=（m2-2m+3）+（m2-m+2）i（m∈R），z2=6+8i，则m=3是z1=z2的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
已知函数f（x）=x3+ax2+bx，（a，b∈R）的图象如图所示，它与直线y=0在原点处相切，此切线与函数图象所围区域（图中阴影部分）的面积为3，则a的值为$-\sqrt{6}$．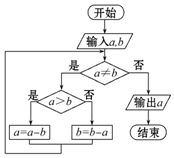
某同学根据“更相减损术”设计出程序框图（图）．若输入a的值为98，b的值为63，则执行该程序框图输出的结果为（ ）