题目内容
(1)2-
+
+
-
(2)log225•log3
•log5
(3)解方程lg(x+1)=1+lg2
(4)求lg14-2lg
+lg7-lg18的值.
| 1 |
| 2 |
| (-4)0 | ||
|
| 1 | ||
|
(1-
|
(2)log225•log3
| 1 |
| 16 |
| 1 |
| 9 |
(3)解方程lg(x+1)=1+lg2
(4)求lg14-2lg
| 7 |
| 3 |
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(1)利用根式与分数指数幂的性质求解.
(2)利用对数的性质和运算法则求解.
(3)由lg(x+1)=1+lg2=lg20,能求出方程的解.
(4)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
(3)由lg(x+1)=1+lg2=lg20,能求出方程的解.
(4)利用对数的性质和运算法则求解.
解答:
解:(1)2-
+
+
-
=
+
+
+1-1
=2
.
(2)log225×log3
×log5
=
×
×
=
×
×
=16.
(3)∵lg(x+1)=1+lg2=lg20,
∴x+1=20,解得x=19.
(4)lg14-2lg
+lg7-lg18
=lg14-lg49+lg9+lg7-lg18
=lg(
)
=lg1=0.
| 1 |
| 2 |
| (-4)0 | ||
|
| 1 | ||
|
(1-
|
=
| ||
| 2 |
| ||
| 2 |
| 2 |
=2
| 2 |
(2)log225×log3
| 1 |
| 16 |
| 1 |
| 9 |
=
| lg25 |
| lg2 |
lg
| ||
| lg3 |
lg
| ||
| lg5 |
=
| 2lg5 |
| lg2 |
| -4lg2 |
| lg3 |
| -2lg3 |
| lg5 |
=16.
(3)∵lg(x+1)=1+lg2=lg20,
∴x+1=20,解得x=19.
(4)lg14-2lg
| 7 |
| 3 |
=lg14-lg49+lg9+lg7-lg18
=lg(
| 14×9×7 |
| 49×18 |
=lg1=0.
点评:本题考查对数和指数的运算,考查对数方程的求解,解题时要认真审题,注意对数和指数的运算法则的合理运用.

练习册系列答案
相关题目
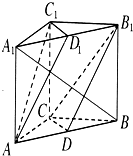 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.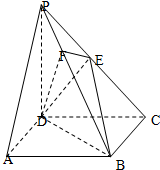 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.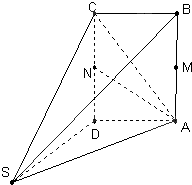 如图,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD=2,M,N分别为AB,CD中点.
如图,多面体ABCDS中,四边形ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD=2,M,N分别为AB,CD中点.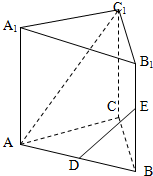 如图,直三棱柱ABC-A1B1C1中,AA1=AC=AB=1,BC=
如图,直三棱柱ABC-A1B1C1中,AA1=AC=AB=1,BC=