题目内容
已知点A、B、C的坐标分别是（4，0）、（0，4）、（3cosα，3sinα），且α∈（
，
）．若
⊥
，求
的值．
| π |
| 2 |
| 3π |
| 4 |
| AC |
| BC |
| 2sin2α+sin2α |
| 1-tanα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由A，B，C的坐标表示出
与
，利用平面向量的数量积运算法则列出关系式，求出sinα+cosα的值，两边平方利用同角三角函数间基本关系求出sin2α的值，根据α的范围求出α+
的范围，进而求出cos（α+
）的值，原式分子提取sinα，分母利用同角三角函数间基本关系化简，整理后将各自的值代入计算即可求出值．
| AC |
| BC |
| π |
| 4 |
| π |
| 4 |
解答：
解：∵
=（3cosα-4，3sinα），
=（3cosα，3sinα-4），且
⊥
，
∴
•
=0，即（3cosα-4）•3cosα+3sinα（3sinα-4）=0，
整理得：sinα+cosα=
，
两边平方得：（sinα+cosα）2=1+2sinαcosα=
，即sin2α=-
，
∵sin（α+
）=
（sinα+cosα）=
，α∈（
，
），即α+
∈（
，π），
∴cos（α+
）=-
，
则原式=
=
=
=
．
| AC |
| BC |
| AC |
| BC |
∴
| AC |
| BC |
整理得：sinα+cosα=
| 3 |
| 4 |
两边平方得：（sinα+cosα）2=1+2sinαcosα=
| 9 |
| 16 |
| 7 |
| 16 |
∵sin（α+
| π |
| 4 |
| ||
| 2 |
3
| ||
| 8 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴cos（α+
| π |
| 4 |
| ||
| 8 |
则原式=
| 2sinα(sinα+cosα) | ||
|
| sin2α(sinα+cosα) | ||||
|
-
| ||||||
|
21
| ||
| 368 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC的中点．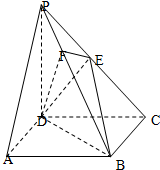
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
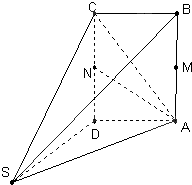如图，多面体ABCDS中，四边形ABCD为矩形，SD⊥AD，SD⊥AB，且AB=2AD=2，M，N分别为AB，CD中点．
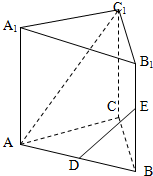如图，直三棱柱ABC-A1B1C1中，AA1=AC=AB=1，BC=