题目内容
3. 如图,四棱锥P-ABCD中,ABCD为平行四边形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,点Q在线段AD上,DQ=1,点M在线段PB上,BP=3BM.
如图,四棱锥P-ABCD中,ABCD为平行四边形,∠ABC=60°,AD=3,PA=AB=2,∠PAD=120°,点Q在线段AD上,DQ=1,点M在线段PB上,BP=3BM.(Ⅰ)证明:AM∥平面PCQ;
(Ⅱ)若平面PAD⊥平面ABCD,求直线AC与平面PCQ所成角的正弦值.
分析 (Ⅰ)在BC上取点N,使CN=2,连接AN,AM,结合已知可得AQCN是平行四边形,得AN∥CQ,则AN∥平面PCQ,再由平行线截线段成比例定理可得MN∥PC,得MN∥平面PCQ,由面面平行的判定可得平面AMN∥平面PCQ,得到AM∥平面PCQ;
(Ⅱ)取PQ中点E,连接AE,可得AE⊥PQ.求解三角形可得CQ⊥AD,由面面垂直的性质得到CQ⊥平面PAD,进一步得到AE⊥平面PCQ,得∠ACE为直线AC与平面PCQ所成角.求解直角三角形得答案.
解答 (Ⅰ)证明:在BC上取点N,使CN=2,连接AN,AM,
∵DQ=1,AD=3,AQ=2=CN,
∴AQCN是平行四边形,则AN∥CQ,
∴AN∥平面PCQ,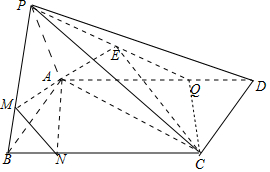
∵$\frac{BN}{BC}=\frac{BM}{BP}$=$\frac{1}{3}$,
∴MN∥PC,则MN∥平面PCQ,有平面AMN∥平面PCQ.
又∵AM?平面AMN,
∴AM∥平面PCQ;
(Ⅱ)解:取PQ中点E,连接AE,
∵PA=AQ,∴AE⊥PQ.
∵QD=1,CD=2,∠CDQ=60°,
∴CQ⊥AD,
∵平面PAD⊥平面ABCD,
∴CQ⊥平面PAD,
∴CQ⊥AE,又AE⊥PQ,
∴AE⊥平面PCQ,
∴∠ACE即为直线AC与平面PCQ所成角.
在Rt△AEC中,
∵AE=1,AC=$\sqrt{A{Q}^{2}+C{Q}^{2}}=\sqrt{7}$.
∴sin∠ACE=$\frac{AE}{AC}=\frac{\sqrt{7}}{7}$.
点评 本题考查线面平行的判定,考查直线与平面所成角,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11.设集合M={x|x2-2x-3≥0},N={x|-3<x<3},则( )
| A. | M⊆N | B. | N⊆M | C. | M∪N=R | D. | M∩N=∅ |
8.已知直线l1:(k+1)x+y+1=0和l2:(k-3)x-ky-1=0,若l1与l2有公共点,则k的取值范围为( )
| A. | k≠1且k≠-3 | B. | k≠-3 | C. | k=1 | D. | k=1且k=-3 |
15.要得到函数y=2cos(5x+$\frac{π}{2}$)的图象,只要把函数y=2cos5x的图象上所有的点( )
| A. | 向左平移$\frac{π}{10}$个单位长度 | B. | 向右平移$\frac{π}{10}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
12.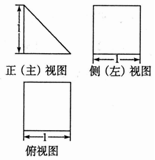 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.证明:CA是△ABC外接圆的直径.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.证明:CA是△ABC外接圆的直径.