题目内容
1.已知函数f(x)=lnx-$\frac{1}{2}$a(x-1)(a∈R).(Ⅰ)若a=-2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若不等式f(x)<0对任意x∈(1,+∞)恒成立,求实数a的取值范围.
分析 (1)一求切点,二求切点处的导数,即切线的斜率;
(2)只需求出函数f(x)在区间[1,+∞)上的最大值即可,利用导数研究单调性,进一步求其最值构造不等式求解;比较大小可将两个值看成函数值,然后利用函数的性质求解.
解答 解:(Ⅰ) 因为a=-2时,f(x)=inx+x-1,f′(x)=$\frac{1}{x}$+1.
所以切点为(1,0),k=f′(1)=2.
所以a=-2时,曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-2.
( II)( i)由f(x)=lnx-$\frac{1}{2}$a(x-1),
所以f′(x)=$\frac{1}{x}$-$\frac{a}{2}$,
①当a≤0时,x∈(1,+∞),f′(x)>0,
∴f(x)在(1,+∞)上单调递增,f(x)>f(1)=0,
∴a≤0不合题意.
②当a≥2即0$<\frac{2}{a}$≤1时,f′(x)=$\frac{1}{x}$-$\frac{a}{2}$<0,在(1,+∞)上恒成立,
∴f(x)在(1,+∞)上单调递减,有f(x)<f(1)=0,
∴a≥2满足题意.
③若0<a<2即$\frac{2}{a}>1$时,由f′(x)>0,可得1<x<$\frac{2}{a}$,由f′(x)<0,可得x$>\frac{2}{a}$,
∴f(x)在$(1,\frac{2}{a})$上单调递增,在$(\frac{2}{a},+∞)$上单调递减,
∴f($\frac{2}{a}$)>f(1)=0,
∴0<a<2不合题意.
综上所述,实数a的取值范围是[2,+∞).
点评 本题主要考查函数、导数、不等式等基本知识;考查运算求解能力、推理论证能力;考查化归与转化思想、函数与方程的思想、分类整合思想、数形结合思想.

练习册系列答案
相关题目
10.函数y=(x-4)|x|在[a,4]上的最小值为-4,则实数a的取值范围是( )
| A. | $[{2-2\sqrt{2},2}]$ | B. | (-∞,2] | C. | $[{2-2\sqrt{2},2})$ | D. | $({2-2\sqrt{2},2})$ |
11.某调查机构为了研究“户外活动的时间长短”与“患感冒”两个分类变量是否相关,在该地随机抽取了若干名居民进行调查,得到数据如表所示:
若从被调查的居民中随机抽取1人,则取到活动时间超过1小时的居民的概率为$\frac{3}{5}$.
(1)完善上述2×2列联表;
(2)能否在犯错误的概率不超过0.1%的前提下,认为“户外活动的时间长短”与“患感冒”两者间相关.
| 患感冒 | 不患感冒 | 合计 | |
| 活动时间超过1小时 | 20 | 40 | 60 |
| 活动时间低于1小时 | 30 | 10 | 40 |
| 合计 | 50 | 50 | 100 |
(1)完善上述2×2列联表;
(2)能否在犯错误的概率不超过0.1%的前提下,认为“户外活动的时间长短”与“患感冒”两者间相关.
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
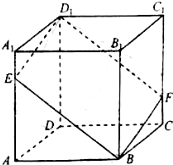 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④