题目内容
16.设函数f(x)=lnx-$\frac{1}{2}$ax2-bx(1)当a=b=$\frac{1}{2}$时,求函数f(x)的单调区间;
(2)设F(x)=f(x)+$\frac{1}{2}$ax2+bx+$\frac{a}{x}$.对任意x∈(0,3],总有F′(x)≤$\frac{1}{2}$成立,求实数a的取值范围;
(3)当a=0,b=-1时,方程f(x)=mx在区间[1,e2]内有唯一实数解,求实数m的取值范围.
分析 (1)求出函数的导数,从而得到函数的单调区间;
(2)求出F(x)的导数,问题转化为a≥x0-$\frac{1}{2}$${{x}_{0}}^{2}$在x0∈(0,3]上恒成立,根据函数的单调性求出a的值即可;
(3)问题转化为只需m=1+$\frac{lnx}{x}$有唯一实数解,令g(x)=1+$\frac{lnx}{x}$,(x>0),求出g(x)的最值,从而求出m的范围即可.
解答 解:(1)当a=b=$\frac{1}{2}$时,f(x)=lnx-$\frac{1}{4}$x2-$\frac{1}{2}$x(x>0),
f′(x)=$\frac{1}{x}$-$\frac{1}{2}$x-$\frac{1}{2}$=$\frac{-(x+2)(x-1)}{2x}$,
易知f(x)在(0,1]上递增,在[1,+∞)上递减,
故f(x)的最大值为f(1)=-$\frac{3}{4}$.(6分)
(2)F(x)=lnx+$\frac{a}{x}$,F′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
由题意 $\frac{{x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$,x0∈(0,3]恒成立,即a≥x0-$\frac{1}{2}$${{x}_{0}}^{2}$在x0∈(0,3]上恒成立.
易知当x0=1时,x0-$\frac{1}{2}$${{x}_{0}}^{2}$取得最大值$\frac{1}{2}$,
故a≥$\frac{1}{2}$;
(3)当a=0,b=-1时,f(x)=lnx+x,
由f(x)=mx,得lnx+x=mx,
又x>0,于是m=1+$\frac{lnx}{x}$,
要使方程f(x)=mx在区间[1,e2]上有唯一实数解,
只需m=1+$\frac{lnx}{x}$有唯一实数解,
令g(x)=1+$\frac{lnx}{x}$,(x>0),于是g′(x)=$\frac{1-lnx}{{x}^{2}}$,
由g′(x)>0,得0<x<e,由g′(x)<0,得x>e,
于是g(x)在区间[1,e]上是增函数,在区间[e,e2]上是减函数,
g(1)=1,g(e2)=1+$\frac{2}{{e}^{2}}$,g(e)=1+$\frac{1}{e}$,
故m=1+$\frac{1}{e}$或1≤m<1+$\frac{2}{{e}^{2}}$.
点评 本题主要考查利用导数求曲线在某点的切线斜率,求二次函数在闭区间上的最值,利用导数求函数在闭区间上的最值,属于中档题.

(1)当a=5时,求函数y=g(x)在x=1处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值.
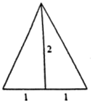
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
(1)根据以上数据建立一个2×2的列联表;
| 看电视 | 运动 | 合计 | |
| 男性 | 21 | ||
| 女性 | 43 | 70 | |
| 合计 | 124 |
参考临界值表
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |