题目内容
9.已知F1(-2,0),F2(2,0)分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,且椭圆C过点(-$\sqrt{3}$,1).(1)求椭圆C的方程;
(2)直线l过椭圆C的右焦点F2且斜率为1与椭圆C交于A,B两点,求弦AB的长;
(3)以第(2)题中的AB为边作一个等边三角形ABP,求点P的坐标.
分析 (1)由已知列关于a,b,c的方程组,求解方程组可得a,b的值,则椭圆方程可求;
(2)写出直线l的方程,联立直线方程和椭圆方程,利用弦长公式求得弦AB的长;
(3)设AB的中点为M(x0,y0),由中点坐标公式求出M的坐标,写出AB的中垂线方程,得到P的坐标,由MP得长度与AB长度的关系列式即可解得点P的坐标.
解答 解:(1)由已知可得$\left\{\begin{array}{l}{c=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{3}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\end{array}\right.$,解得a2=6,b2=2.
∴椭圆C的方程的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;
(2)由(1)知,F2(2,0),则直线l的方程为y=x-2,
联立$\left\{\begin{array}{l}{y=x-2}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得2x2-6x+3=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=3,{x}_{1}{x}_{2}=\frac{3}{2}$,
∴|AB|=$\sqrt{2}|{x}_{1}-{x}_{2}|=\sqrt{2}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}•\sqrt{{3}^{2}-4×\frac{3}{2}}=\sqrt{6}$;
(3)设AB的中点为M(x0,y0).
∵x1+x2=3=2x0,∴${x}_{0}=\frac{3}{2}$,
∵y0=x0-2,∴${y}_{0}=\frac{1}{2}$.
线段AB的中垂线l1斜率为-1,∴l1:y=-x+1,
设P(t,1-t),∴|MP|=$\sqrt{(t-\frac{3}{2})^{2}+(\frac{3}{2}-t)^{2}}$=$\sqrt{2}|t-\frac{3}{2}|$|,
当△ABP为正三角形时,|MP|=$\frac{\sqrt{3}}{2}$|AB|,
得$\sqrt{2}|t-\frac{3}{2}|$=$\frac{\sqrt{3}}{2}×\sqrt{6}$,解得t=0或3.
∴P(0,1),或P(3,-2).
点评 本题考查椭圆方程的求法,考查弦长公式的应用,考查数学转化思想方法,是中档题.

| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -1 | D. | 1 |
| A. | 1007 | B. | 1008 | C. | 2015 | D. | 2016 |
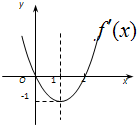 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
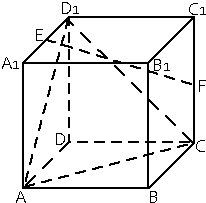 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.