题目内容
13.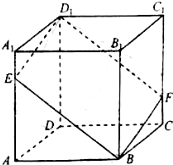 已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④
已知正方体ABCD-A1B1C1D1,如图,E是棱AA1上动点,过点D1,E,B作该正方体的截面与棱CC1交于点F.设AE=x,则下列关于四棱锥B1-BFD1E的命题,其中正确的序号有③④①底面BFD1E的面积随着x增大而增大;
②四棱锥B1-BFD1E的体积随着x增大先增大后减少;
③底面BFD1E的面积随着x增大先减少后增大;
④四棱锥B1-BFD1E的体积与x取值无关,且总保持恒定不变.
分析 设正方体的棱长为a,由图形可知,当x=0或x=a时,四边形BFD1E的面积取得最大值为$\sqrt{2}{a}^{2}$,当x=$\frac{a}{2}$时,四边形BFD1E的面积有最小值为$\frac{\sqrt{6}}{2}{a}^{2}$,由此判断①错误,③正确;再利用等积法证明四棱锥B1-BFD1E的体积与x取值无关,说明②错误,④正确.
解答 解:由图可知,四边形BFD1E是平行四边形,
设正方体的棱长为a,AE=x(0≤x≤a),
则当x=0或x=a时,四边形BFD1E的面积取得最大值为$\sqrt{2}{a}^{2}$,
当x=$\frac{a}{2}$时,四边形BFD1E的面积有最小值为$\frac{\sqrt{6}}{2}{a}^{2}$.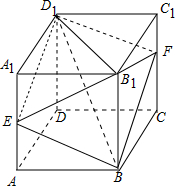
∴①错误,③正确;
四棱锥B1-BED1F的体积等于${V}_{{D}_{1}-B{B}_{1}E}+{V}_{{D}_{1}-B{B}_{1}F}$,
∵三角形BB1E的面积为$\frac{1}{2}{a}^{2}$为定值,三棱锥D1-BB1E的高D1C1=a,
三角形BB1F的面积为$\frac{1}{2}{a}^{2}$为定值,三棱锥D1-BB1F的高为D1A1=a,
∴三棱锥D1-BB1E和三棱锥D1-BB1F体积为定值,
即四棱锥B1-BED1F的体积为定值,
∴②错误,④正确.
∴正确命题的序号是③④.
故答案为:③④.
点评 本题考查命题的真假判断与应用,考查了利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
8.若一个正三棱锥的正(主)视图如图所示,则其体积等于( )
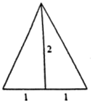

| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
3.已知函数f(x)=$\frac{1}{3}{x^3}$+ax2+(a+2)x-3有两个极值点,则实数a的取值范围是( )
| A. | (-1,2) | B. | (-∞,-1)∪(2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |
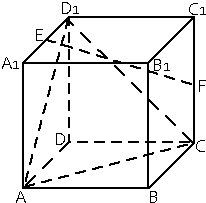 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.