题目内容
11.已知数列{an}是首项为a,公差为b的等差数列,数列{bn}是首项为b,公比为a的等比数列,且a1<b1<a2<b2<a3,其中a,b,m,n∈N*.(Ⅰ)求a的值;
(Ⅱ)若数列{1+am}与数列{bn}有公共项,将所有公共项按原来顺序排列后构成一个新数列{cn},求数列{cn}的通项公式;
(Ⅲ)设dm=$\frac{a_m}{2m}$,m∈N*,求证:$\frac{1}{{1+{d_1}}}$+$\frac{2}{{(1+{d_1})(1+{d_2})}}$+…+$\frac{n}{{(1+{d_1})(1+{d_2})…(1+{d_n})}}$<2.
分析 (Ⅰ)由题设am=a+(m-1)b,知bn=b•an-1.由a<b<a+b<ab<a+2b,知ab<a+2b<3b.由此能求出a.
(Ⅱ)设1+a+(m-1)b=b•an-1.由a=2,知3+(m-1)b=b•2n-1,得到b=$\frac{3}{{2}^{n-1}-(m-1)}$..由此能求出cn.
(Ⅲ)先用放缩法得到dm=$\frac{a_m}{2m}$≥1,再用基本不等式得到1+di≥2$\sqrt{{d}_{i}}$>0,i=1,2,…,k,用累乘法并化简可得不等式的左边,再放缩,得到左边≤$\frac{1}{2}$+$\frac{{2}^{\;}}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,设Sn=$\frac{1}{2}$+$\frac{{2}^{\;}}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,利用错位相减法求和,最后放缩即可证明.
解答 解:(I)∵am=a+(m-1)b,bn=b•an-1,
由已知可得,a<b<a+b<ab<a+2b
∴b<ab,a>1
∴ab<a+2b<3b
又∵b>0
∴a<3
∵a为正整数
∴a=2
(II)设1+am=bn,即1+a+(m-1)b=b•an-1.
∴3+(m-1)b=b•2n-1,b=$\frac{3}{{2}^{n-1}-(m-1)}$.
∵b>a=2,且b∈N*,
∴2n-1-(m-1)=1.
∴2n-1=m,且b=3
∴cn=bn=3•2n-1.
(III)证明:由(I)(II)可得am=a+b(m-1),且a=2,b>2,
可知a1=2,
当m≥2时,am≥2m,
∴dm=$\frac{a_m}{2m}$≥1,
∴对任意正整数k,均有d1•d2…dk≥1
由基本不等式可得1+di≥2$\sqrt{{d}_{i}}$>0,i=1,2,…,k,
累乘可得(1+d1)(1+d2)…(1+dk)≥2k,
则:$\frac{1}{{1+{d_1}}}$+$\frac{2}{{(1+{d_1})(1+{d_2})}}$+…+$\frac{n}{{(1+{d_1})(1+{d_2})…(1+{d_n})}}$≤$\frac{1}{2}$+$\frac{{2}^{\;}}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,
令Sn=$\frac{1}{2}$+$\frac{{2}^{\;}}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,
则$\frac{1}{2}$Sn=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,
∴$\frac{1}{2}$Sn=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$,
∴Sn=2-$\frac{2}{{2}^{n}}$-$\frac{n}{{2}^{n}}$<2,
∴$\frac{1}{{1+{d_1}}}$+$\frac{2}{{(1+{d_1})(1+{d_2})}}$+…+$\frac{n}{{(1+{d_1})(1+{d_2})…(1+{d_n})}}$<2.
点评 本题考查数列的综合运用,解题时要认真审题,仔细解答,合理地运用放缩法进行证明.注意挖掘题设中的隐含条件,合理地进行等价转化,属于难题.

| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -1 | D. | 1 |
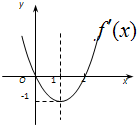 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)