题目内容
10.函数y=(x-4)|x|在[a,4]上的最小值为-4,则实数a的取值范围是( )| A. | $[{2-2\sqrt{2},2}]$ | B. | (-∞,2] | C. | $[{2-2\sqrt{2},2})$ | D. | $({2-2\sqrt{2},2})$ |
分析 先作出函数y=(x-2)|x|在a≤x≤2上的图象,结合函数图象,欲使函数y=(x-2)|x|在a≤x≤2上的最小值为-1,则xA≤a≤xB,从而求出所求
解答 解:y=(x-4)|x|=$\left\{\begin{array}{l}{x}^{2}-4x,x≥0\\-{x}^{2}+4x,x<0\end{array}\right.$,
作出函数y=(x-2)|x|在a≤x≤4上的图象,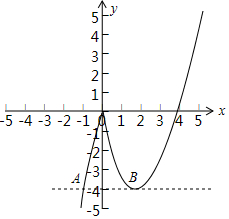
令(x-4)|x|=-4,
当x≥0时,x2-4x=-4,解得xB=2,
当x<0时,-x2+4x=-4,解得xA=2-2$\sqrt{2}$,
结合函数图象,欲使函数y=(x-4)|x|在[a,4]上的最小值为-4,则xA≤a≤xB,
即实数a的取值范围为$[{2-2\sqrt{2},2}]$,
故选:A
点评 本题主要考查了分段函数的应用,以及函数最值的应用,同时考查了作图的能力和数形结合的思想,属于中档题.

练习册系列答案
相关题目
20.若直线x+y-1=0与抛物线y=2x2交于A,B两点,则点M(1,0)到A,B两点的距离之积为( )
| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |
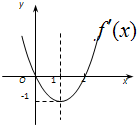 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)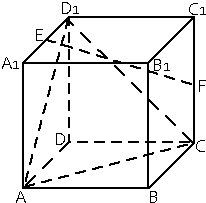 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.