题目内容
12.点P到A(-2,0)的距离是点P到B(1,0)的距离的2倍.(Ⅰ)求点P的轨迹方程;
(Ⅱ)点P与点Q关于点(2,1)对称,点C(3,0),求|QA|2+|QC|2的最大值和最小值.
(Ⅲ)若过A的直线从左向右依次交第(II)问中Q的轨迹于不同两点E,F,$\overrightarrow{FA}$=λ$\overrightarrow{EA}$,判断λ的取值范围并证明.
分析 (Ⅰ)利用直接法,求点P的轨迹方程;
(Ⅱ)求出Q的轨迹方程,令z=|QA|2+|QC|2=(x+2)2+y2+(x-3)2+y2=6x+8y+5,所以6x+8y+5-z=0,利用直线与圆的位置关系,即可求|QA|2+|QC|2的最大值和最小值;
(Ⅲ)设过A的直线方程为x=ty-2(一定存在),与Q的轨迹方程联立,消去x得(1+t2)y2-(8t+4)y+16=0,利用韦达定理,结合基本不等式,即可得出结论.
解答 解:(I)设点P(x,y),由题意可得|PA|=2|PB|,即$\sqrt{(x+2)^{2}+{y}^{2}}$=2$\sqrt{(x-1)^{2}+{y}^{2}}$.
化简可得(x-2)2+y2=4.(4分)
(II)设Q(x0,y0),由题可得x=4-x0,y=2-y0代入上式消去可得(x0-2)2+(y0-2)2=4,即Q的轨迹方程为(x-2)2+(y-2)2=4,即x2+y2+4=4x+4y.(6分)
令z=|QA|2+|QC|2=(x+2)2+y2+(x-3)2+y2=6x+8y+5,所以6x+8y+5-z=0,
d=$\frac{|33-z|}{10}$≤2,所以13≤z≤53.
因此|QA|2+|QC|2的最大值为53,最小值为13.(9分)
(III)λ的取值范围是(1,$\frac{3+\sqrt{5}}{2}$].(10分)
证明:设E(x1,y1),F(x2,y2)且y1<y2.
因为$\overrightarrow{FA}$=λ$\overrightarrow{EA}$,所以$\left\{\begin{array}{l}{{x}_{2}+2=λ({x}_{1}+2)}\\{{y}_{2}=λ{y}_{1}}\end{array}\right.$,且λ>1.(11分)
设过A的直线方程为x=ty-2(一定存在),与Q的轨迹方程联立,消去x得(1+t2)y2-(8t+4)y+16=0.
△>0,解得t>$\frac{3}{4}$.
而y1+y2=$\frac{8t+4}{1+{t}^{2}}$,y1y2=$\frac{16}{1+{t}^{2}}$,$\frac{{y}_{1}}{{y}_{2}}+\frac{{y}_{2}}{{y}_{1}}$+2=$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$,
因此$λ+\frac{1}{λ}$+2=4+$\frac{4t-3}{1+{t}^{2}}$=4+$\frac{16}{(4t-3)+\frac{25}{4t-3}+6}$≤5,当且仅当t=2时等号成立.
所以$λ+\frac{1}{λ}$-3≤0(k>1),解得1<λ≤$\frac{3+\sqrt{5}}{2}$.(14分)
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

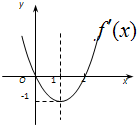 已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)
已知函数f(x)的导函数f′(x)的图象如图,下列说法正确的是④ (只填序号)