题目内容
(1)化简:(2a
b
)(-6a
b
)÷(-3a
b
);
(2)已知log83=p,log35=q,则lg5的值为多少?(用p、q表示).
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
(2)已知log83=p,log35=q,则lg5的值为多少?(用p、q表示).
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用指数的运算性质即可得出;
(2)利用对数的运算性质、lg2+lg5=1即可得出.
(2)利用对数的运算性质、lg2+lg5=1即可得出.
解答:
解(1)原式=
=4a
-
•b
-
=4a.
(2)∵log83=p,log35=q,
∴
=p,
=q.
∴
=pq,
∴lg5=3(1-lg5)pq,
解得lg5=
.
-12a
| ||||||||
-3a
|
| 7 |
| 6 |
| 1 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
(2)∵log83=p,log35=q,
∴
| lg3 |
| 3lg2 |
| lg5 |
| lg3 |
∴
| lg5 |
| 3lg2 |
∴lg5=3(1-lg5)pq,
解得lg5=
| 3pq |
| 1+3pq |
点评:本题考查了指数的运算性质、对数的运算性质、lg2+lg5=1,属于基础题.

练习册系列答案
相关题目
下列函数在其定义域上既是奇函数又是增函数的是( )
| A、y=x-1 | ||||
B、y=-
| ||||
C、y=
| ||||
D、y=-
|
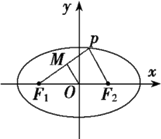 P为椭圆
P为椭圆 设函数f(x)=ax3-2bx2+cx+4d(a、b、c、d∈R)图象关于原点对称,且当x=1时,f(x)取极小值-
设函数f(x)=ax3-2bx2+cx+4d(a、b、c、d∈R)图象关于原点对称,且当x=1时,f(x)取极小值-