题目内容

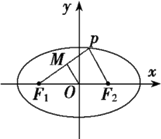P为椭圆
x2
25
+
y2
16
=1上任意一点，F1，F2为左右焦点．如图所示：
（1）若PF1的中点为M，求证：|MO|=5-
1
2
|PF1|
（2）若∠F1PF2=60°，求|PF1|•|PF2|的值．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）利用椭圆的定义，结合中位线的性质，即可得出结论；
（2）利用余弦定理，结合椭圆的定义，即可求|PF1|•|PF2|的值．
解答： （1）证明：在△F1PF2中，MO为中位线，
∴|MO|=
|PF2|
2
=
2a-|PF1|
2
=a-
|PF1|
2
=5-
1
2
|PF1|…（5分）
（2）解：∵|PF1|+|PF2|=10，∴|PF1|2+|PF2|2=100-2|PF1|•|PF2|
在△PF1F2中，cos60°=
|PF1|2+|PF2|2-|F1F2|2
2|PF1||PF2|
，
∴|PF1||PF2|=100-2|PF1||PF2|-36，
∴|PF1||PF2|=
64
3
…（12分）
点评：本题考查椭圆的定义，考查余弦定理的运用，考查学生分析解决问题的能力，正确运用椭圆的定义是关键．
练习册系列答案
相关题目
曲线x2+y2=|x|+|y|所围成的面积为（　　）
A、
π
2
+1
B、π+2
C、2π+1
D、均不对
△ABC中，a，b，c分别是∠A，∠B，∠C的对边，且4sin2
B+C
2
-cos2A=
7
2
．
（1）求∠A；
（2）若b=3，c=3，求边a．
已知椭圆
y2
a2
+
x2
b2
=1（a＞b＞0）的离心率e=
3
2
，且经过点（
3
2
，1）．
（Ⅰ）求椭圆的方程；
（Ⅱ）直线l过椭圆的上焦点，交椭圆于A（x1，y1），B（x2，y2）两点，已知
m
=（ax1，by1），
n
=（ax2，by2），若
m
⊥
n
，求直线l的斜率k的值．
已知奇函数f（x）=ax3+bx2+cx（a≠0）在x=1处取得极大值2．
（1）求函数y=f（x）的解析式；
（2）对于区间[-2，2]上任意的x1，x2，都有|f（x1）-f（x2）|≤c，求实数c的最小值；
（3）过点M（2，m）（m≠2）可作y=-f（x）的三条切线，求实数m的取值范围．
（1）化简：（2a
2
3
b
1
2
）（-6a
1
2
b
1
3
）÷（-3a
1
6
b
5
6
）；
（2）已知log83=p，log35=q，则lg5的值为多少？（用p、q表示）．
已知全集为R，集合A={x|2≤x＜4}，B={x|3x-7≥8-2x}，求：
（1）A∩B；
（2）（∁RA）∩（∁RB）．
已知：f（x）=cos2x+2
3
sinxcosx-sin2x，求：
（1）f（x）的最小正周期；
（2）当x∈[0，
π
2
]时，求函数f（x）的最大、最小值．
已知数列{an}的前n项和为Sn=-n2+2kn（k∈N+），且Sn的最大值为4．
（1）求数列{an}的通项an；
（2）令bn=
5-an
2n
，求数列{bn}的前n项和．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网