题目内容
（选做题）若对任意x∈R，|x-a|+|x+1|≥3恒成立，则实数a的取值范围是 ．
考点：函数恒成立问题,绝对值三角不等式
专题：不等式的解法及应用
分析：利用绝对值的意义，结合绝对值不等式的性质，求出左边式子的最小值，即可解决问题．
解答：
解：原式左边=|x-a|+|x+1|≥|（x-a）-（x+1）|=|a+1|．
则要使原式对任意的实数x恒成立，只需|a+1|≥3，
即a+1≥3或a+1≤-3．
解得a≥2或a≤-4．
故答案为a≥2或a≤-4．
则要使原式对任意的实数x恒成立，只需|a+1|≥3，
即a+1≥3或a+1≤-3．
解得a≥2或a≤-4．
故答案为a≥2或a≤-4．
点评：本题考查了绝对值不等式性质，以及不等式恒成立问题的解题思路，此类问题常转化为函数的最值问题来解．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=
的图象关于（ ）对称．
| 1 |
| x |
| A、x轴 | B、y轴 | C、原点 | D、y=1 |
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，求时速在[60，70]的汽车大约有多少辆？已知ξ的分布列为：
则Dξ等于（ ）
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
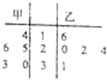将甲、乙两名篮球运动员在篮球比赛中的得分制成茎叶图如图所示，若. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
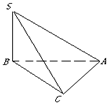三棱锥S-ABC中，∠SBA=∠SCA=90°，△ABC是斜边AB=a的等腰直角三角形，SB=a，则以下结论中：