题目内容
3.已知a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}}$,b=($\frac{1}{3}$)${\;}^{-\frac{1}{2}}}$,c=log2$\frac{1}{3}$,则a,b,c的大小关系是( )| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
分析 利用指数式和对数式的性质,比较三个数与0或1的大小得答案.
解答 解:∵0<$a=(\frac{1}{2})^{\frac{1}{3}}={2}^{-\frac{1}{3}}$<1,
$b=(\frac{1}{3})^{-\frac{1}{2}}={3}^{\frac{1}{2}}$>1,
$c={log_2}\frac{1}{3}$<log21=0,
∴c<a<b.
故选:A.
点评 本题考查对数值的大小比较,关键是注意利用0和1为媒介,是基础题.

练习册系列答案
相关题目
15.若函数f(x)=sinx+cosx,则f′($\frac{π}{2}$)的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
12.已知$f(x)=\left\{\begin{array}{l}a-{x^2}-2x,x≤0\\{e^{|x-1|}},x>0\end{array}\right.$,且函数y=f(x)-1恰有3个不同的零点,则实数a的取值范围是( )
| A. | (-1,+∞) | B. | (-2,0) | C. | (-2,+∞) | D. | (0,1] |
 如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.
如图,一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距灯塔60海里的M处,下午2时到达这座灯塔的东偏南45°的N处,则该船航行的速度为$\frac{15\sqrt{6}}{2}$海里/小时.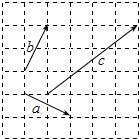 如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.
如图,在6×6的方格中,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$的起点和终点均在格点,且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),那么x+y=3.