��Ŀ����
2��ij������ѧ��ѧ��111�ˣ�����һ�꼶108�ˣ��������꼶��81�ˣ���Ҫ���ó�������ȡ10�˲μ�ij����飬����ѡ�ü�����������ֲ������ϵͳ�������ַ�����ʹ�ü���������ͷֲ����ʱ����ѧ����һ���������꼶����ͳһ���Ϊ1��2������270��ʹ��ϵͳ����ʱ����ѧ��ͳһ������1��2������270����������������η�Ϊ10�� �����ú��������������������7��34��61��88��115��142��169��196��223��250��
��5��9��100��107��111��121��180��195��200��265��
��11��38��65��92��119��146��173��200��227��254��
��30��57��84��111��138��165��192��219��246��270��
�����������������н����У���ȷ���ǣ�������
| A�� | �ڡ��۶�����Ϊϵͳ���� | B�� | �ڡ��ܶ�����Ϊ�ֲ���� | ||
| C�� | �١��۶�����Ϊ�ֲ���� | D�� | �١��ܶ�����Ϊϵͳ���� |
���� �����������������ݵ��ص㣬���ϵͳ�����и����ݵļ������ȵģ������������ֲ����û����һ�������������ɵó����ۣ�
��� �⣺�۲��������������ݣ�
�٣������������еķֶμ����ȣ�������ϵͳ������ֲ������
�ڸ��������и����ݵļ��û�й��ɣ�Ӧ�Ǽ����������
�ܸ��������зֶμ��û�й��ɣ�Ӧ�ò���ϵͳ�����ͷֲ������
�ɴˣ������������ѡ��C��
��ѡ��C��
���� ���⿼���˼����������ϵͳ�������ֲ����������Ӧ�����⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
13��������P��0��-1����ֱ��l����ֱ��l������A��1��-2����B��2��1�����߶�û�й����㣬��ֱ��l��б��k����б�Ǧ���ȡֵ��Χ�ֱ��ǣ�������
| A�� | ��-�ޣ�-1���ȣ�1��+�ޣ�����$\frac{��}{4}$��$\frac{3��}{4}$�� | B�� | ��-�ޣ�-1���ȣ�1��+�ޣ�����$\frac{��}{4}$��$\frac{��}{2}$���ȣ�$\frac{��}{2}$��$\frac{3��}{4}$�� | ||
| C�� | ��-1��1����[$\frac{��}{4}$��$\frac{3��}{4}$] | D�� | ��-1��1����[0��$\frac{��}{4}$]��[$\frac{3��}{4}$��0�� |
17��������N*�ĺ���f��x������f��1��=2����f��n+1��=$\left\{\begin{array}{l}\frac{1}{2}f��n����nΪż��\\ f��n����nΪ����\end{array}$����f��12����ֵΪ��������
| A�� | $\frac{1}{32}$ | B�� | $\frac{1}{16}$ | C�� | $\frac{1}{64}$ | D�� | 1 |
14���ݺ���y=x3��[1��2]�ϵ����ֵ����Сֵ֮��Ϊ��������
| A�� | 10 | B�� | 9 | C�� | 8 | D�� | 6 |
11����֪|$\overrightarrow{a}$|=1��|$\overrightarrow{b}$|=2����$\overrightarrow{a}$��$\overrightarrow{b}$��=60�㣬��|$\overrightarrow{a}$-$\overrightarrow{b}$|=��������
| A�� | 1 | B�� | 2 | C�� | $\sqrt{3}$ | D�� | 4 |
12���㷨�����ͼ��ͼ��ʾ����$a=\frac{��}{2}$��$b={3^{\frac{1}{3}}}$��$c={��{\sqrt{e}}��^{ln3}}$��������Ľ���ǣ�������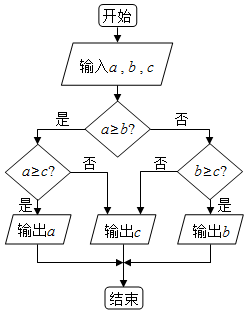

| A�� | $\frac{a+b+c}{3}$ | B�� | a | C�� | b | D�� | c |
 ��ͼ����֪����̨ABCD-A1B1C1D1���ϡ��µ���ֱ��DZ߳�Ϊ3��6�������Σ�AA1=6����A1A�͵���ABCD����P��Q�ֱ�����DD1��BC�ϣ�BQ=4��
��ͼ����֪����̨ABCD-A1B1C1D1���ϡ��µ���ֱ��DZ߳�Ϊ3��6�������Σ�AA1=6����A1A�͵���ABCD����P��Q�ֱ�����DD1��BC�ϣ�BQ=4��