题目内容
15.已知数列{an}中,a1=2,an=3an-1+2(n≥2,n∈N*),数列{bn}中,bn=an+1.(Ⅰ)证明数列{bn}是等比数列,并求其通项公式;
(Ⅱ)若cn=$\frac{{b}_{n}}{({b}_{n}+1)({b}_{n}+3)}$,求数列{cn}的前n项和Sn.
分析 (I)数列{an}中,a1=2,an=3an-1+2(n≥2,n∈N*),bn=an+1.代入:bn+1=an+1+1即可证明.
(II)cn=$\frac{{3}^{n}}{({3}^{n}+1)({3}^{n}+3)}$=$\frac{{3}^{n-1}}{({3}^{n-1}+1)({3}^{n}+1)}$=$\frac{1}{2}$$(\frac{1}{{3}^{n-1}+1}-\frac{1}{{3}^{n}+1})$,利用“裂项求和”方法即可得出.
解答 (I)证明:数列{an}中,a1=2,an=3an-1+2(n≥2,n∈N*),bn=an+1.
∴bn+1=an+1+1=3an+3=3(an+1)=3bn,
∴数列{bn}是等比数列,首项与公比都为3.
∴bn=3n.
(II)解:cn=$\frac{{b}_{n}}{({b}_{n}+1)({b}_{n}+3)}$=$\frac{{3}^{n}}{({3}^{n}+1)({3}^{n}+3)}$=$\frac{{3}^{n-1}}{({3}^{n-1}+1)({3}^{n}+1)}$=$\frac{1}{2}$$(\frac{1}{{3}^{n-1}+1}-\frac{1}{{3}^{n}+1})$,
∴数列{cn}的前n项和Sn=$\frac{1}{2}[(\frac{1}{2}-\frac{1}{3+1})$+$(\frac{1}{3+1}-\frac{1}{{3}^{2}+1})$+…+$(\frac{1}{{3}^{n-1}+1}-\frac{1}{{3}^{n}+1})]$
=$\frac{1}{2}(\frac{1}{2}-\frac{1}{{3}^{n}+1})$.
点评 本题考查了等比数列的通项公式、“裂项求和”方法、递推关系,考查了推理能力与计算能力,属于中档题.

| A. | $\overrightarrow{a}-\overrightarrow{b}$ | B. | $\overrightarrow{a}+\overrightarrow{b}$ | C. | $\overrightarrow{b}-\overrightarrow{a}$ | D. | 不能确定 |
| A. | 1+i | B. | 1-i | C. | $\frac{1+i}{2}$ | D. | $\frac{1-i}{2}$ |
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、③都可能为分层抽样 | D. | ①、④都可能为系统抽样 |
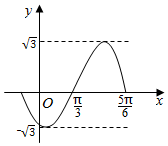 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则g(x)=f(x)+f($\frac{π}{4}$+x)的单调递增区间是[kπ-$\frac{π}{24}$,kπ+$\frac{11π}{24}$],k∈Z.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,则g(x)=f(x)+f($\frac{π}{4}$+x)的单调递增区间是[kπ-$\frac{π}{24}$,kπ+$\frac{11π}{24}$],k∈Z.