题目内容
4.若方程2ax2-x-1=0在(0,1)内恰有一个零点,则有( )| A. | a<-1 | B. | a>1 | C. | -1<a<1 | D. | 0≤a<1 |
分析 由函数零点存在性质定理得f(0)f(1)<0,由此能求出结果.
解答 解:∵方程2ax2-x-1=0在(0,1)内恰有一个零点,
f(0)=-1,f(1)=2a-1-1=2a-2,
∴f(1)=2a-2>0,解得a>1.
故选:B.
点评 本题考查满足条件的这数值的求法,是基础题,解题时要认真审题,注意函数零点存在性质定理的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
16.设全集为R,函数$f(x)=\sqrt{4-{x^2}}$的定义域为M,则∁RM为( )
| A. | [-2,2] | B. | (-2,2) | C. | (-∞,-2]∪[2,+∞) | D. | (-∞,-2)∪(2,+∞) |
13.已知点Q(2$\sqrt{2}$,0)及抛物线x2=4y上一动点P(x,y),则y+|PQ|的最小值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
14.在等比数列{an}中,a1=1,则“a2=4”是“a3=16”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
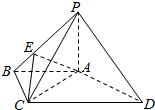 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.