题目内容
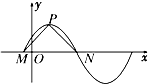如图所示，点P是函数y=2sin（ωx+φ）（x∈R，ω＞0）的图象的最高点，M，N是该图象与x轴的交点，若| PM |
| PN |
A、
| ||
B、
| ||
| C、4 | ||
| D、8 |
考点：正弦函数的图象,平面向量数量积的运算
专题：三角函数的图像与性质
分析：首先判定△MPN为等腰直角三角形，然后通过它的性质求出MN的长度，再求出周期T，进而求得ω．
解答：
解：因为
•
=0，
⊥
，
则△MPN是等腰直角三角形，
又点P到MN的距离为2，所以MN=2×2=4，
则周期T=2×4=8，所以ω=
=
．
故选：B．
| PM |
| PN |
| PM |
| PN |
则△MPN是等腰直角三角形，
又点P到MN的距离为2，所以MN=2×2=4，
则周期T=2×4=8，所以ω=
| 2π |
| T |
| π |
| 4 |
故选：B．
点评：本题主要考查正弦型函数的轴对称性及直角三角形的性质，属于基本知识的考查．
练习册系列答案
相关题目
已知函数f（x）的图象是连续不断的一条曲线，且满足 f（1）＞0，f（5）＜0，若 f（3）＞0．则f（x）在下列区间内必有零点的是（ ）
| A、（1，3） |
| B、（3，5） |
| C、（2，4） |
| D、（3，4） |
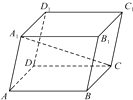如图所示，在平行六面体ABCD-A1B1C1D1中，若| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| A1C |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|