题目内容
在△AOB中,G为△AOB的重心(三角形中三边上中线的交点叫重心),且∠AOB=60°.若
•
=6,则|
|的最小值是 .
| OA |
| OB |
| OG |
考点:平面向量数量积的运算
专题:计算题,不等式的解法及应用,平面向量及应用
分析:设AB的中点为C,则点G在OC上,运用重心的性质和中点向量的表示,再由向量的数量积的定义,结合基本不等式即可求得最小值.
解答:
解:设AB的中点为C,则点G在OC上,
且
=
=
•
=
(
+
),
∵
•
=||
|•|
|•cos60°=6,
∴|
|•|
|=12.
则|
|=
(|
+
|=
=
=
≥
=
×
=2,
当且仅当|
|=|
|时,等号成立,故|
|的最小值是2,
故答案为:2.
且
| OG |
| 2 |
| 3 |
| OC |
| 2 |
| 3 |
| ||||
| 2 |
| 1 |
| 3 |
| OA |
| OB |
∵
| OA |
| OB |
| OA |
| OB |
∴|
| OA |
| OB |
则|
| OG |
| 1 |
| 3 |
| OA |
| OB |
| 1 |
| 3 |
(
|
| 1 |
| 3 |
|
=
| 1 |
| 3 |
|
|
| 1 |
| 3 |
2|
|
| 1 |
| 3 |
| 2×12+12 |
当且仅当|
| OA |
| OB |
| OG |
故答案为:2.
点评:本题主要考查三角形的重心的定义和性质,考查向量的数量积的定义和性质及模,基本不等式的应用,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
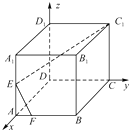 在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1棱长为2,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则点F的坐标为( )
在如图所示的空间直角坐标系中,正方体ABCD-A1B1C1D1棱长为2,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则点F的坐标为( )A、(2,
| ||
B、(2,
| ||
C、(2,
| ||
D、(2,
|
已知点A(-3,1,5)与点B(0,2,3),则A,B之间的距离为( )
A、
| ||
B、2
| ||
C、
| ||
D、
|
函数y=
的值域是( )
|
| A、R |
| B、[0,+∞) |
| C、[-1,+∞) |
| D、(-1,+∞) |
设集合A={x|x2-x-2≤0},B={1,2,3},那么A∩B=( )
| A、{-1,0,1,2,3} |
| B、{-1,0,3} |
| C、{1,2,3} |
| D、{1,2} |
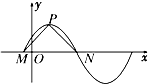 如图所示,点P是函数y=2sin(ωx+φ)(x∈R,ω>0)的图象的最高点,M,N是该图象与x轴的交点,若
如图所示,点P是函数y=2sin(ωx+φ)(x∈R,ω>0)的图象的最高点,M,N是该图象与x轴的交点,若