题目内容

已知a∈R，复数z=（a-2i）（1+i）（i为虚数单位）在复平面内对应的点为M，则“a=0”是“点M在第四象限”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分必要条件的定义进行判断即可．
解答： 解：若a=0，则z=-2i（1+i）=2-2i，点M在第四象限，是充分条件，
若点M在第四象限，则z=（a+2）+（a-2）i，推出-2＜a＜2，推不出a=0，不是必要条件；
故选：A．
点评：本题考查了充分必要条件，考查了复数问题，是一道基础题．
练习册系列答案
相关题目
已知平面直角坐标系xoy上的区域D由不等式
0≤x≤
2
y≤2
y≥
2
2
x
给定，若M（x，y）为D上任一点，点A的坐标为（
2
，1），则z=
OM
•
OA
的最大值为（　　）
A、3
B、4
C、3
2
D、4
2
直线l过点P（2，1）且与x，y轴正半轴分别交于A（a，0），B（0，b）两点，若点（a，b）在y=
x
2
上，则直线l的方程是
 
．
已知x，y分别满足xx=e2，y+lny=ln2，则xy=
 
．
已知i是虚数单位，则复数z=（3-2i）（2+i）在复平面中对应的点位于
 
．
tan(2π-α)sin(-2π-α)cos(6π-α)
cos(α-π)sin(5π-a)
．
设a，b为实数，命题甲：a＜b＜0，命题乙：ab＞b2，则命题甲是命题乙的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
函数y=2+logax，（a＞0且a≠1）必过定点
 
．
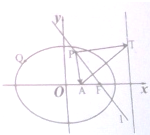如图，Q为椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）上一动点，F（2，0）为椭圆E的右焦点．QF的最小值为1，最大值为5，点A（1，0），点T为直线x=4上一动点，过F点的直线l与AT垂直，l上一点P满足
PA
•
PT
=0．
（1）AP长是否为定值？若是，求出该定值，若不是，说明理由．
（2）求PQ最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网