题目内容
正四棱锥S-ABCD的底面边长4，各侧棱长2
，则外接球体积为 ．
| 7 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：画出图形，正四棱锥外接球的球心在它的高上，然后根据勾股定理解出球的半径，最后根据球的体积公式解之即可．
解答：
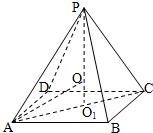解：正四棱锥P-ABCD的外接球的球心在它的高PO1上，
记球心为O，PO=AO=R，PO1=2
，OO1=R-2
，或OO1=2
-R（此时O在PO1的延长线上），
在Rt△AO1O中，R2=8+（R-2
）2得R=
，∴球的体积V=
π•(
)3=
π
故答案为：
π．
解：正四棱锥P-ABCD的外接球的球心在它的高PO1上，记球心为O，PO=AO=R，PO1=2
| 5 |
| 5 |
| 5 |
在Rt△AO1O中，R2=8+（R-2
| 5 |
| 7 | ||
|
| 4 |
| 3 |
| 7 | ||
|
1372
| ||
| 75 |
故答案为：
1372
| ||
| 75 |
点评：本题主要考查球的体积，球的内接体问题，考查计算能力和空间想象能力，属于中档题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
直线a，b?平面α，且a，b成的角为40°，经过α外一点A与a，b都成30°角的直线有且只有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
时间经过10分钟，钟表的分针旋转过程中形成的角的弧度数是（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
sin（-
π）的值等于（ ）
| 14 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|