题目内容
9.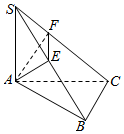 如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.
如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.
分析 (1)由SA⊥底面ABC,即可证明BC⊥SA,由已知及勾股定理即可证明AB⊥BC,从而可证BC⊥面SAB;
(2)由(1)可证BC⊥AE,又AE⊥SB,从而可证AE⊥面SBC.
解答 证明:(1)∵SA⊥底面ABC,BC?底面ABC,
∴BC⊥SA,
又∵AB=3,BC=4,AC=5,可得:AB2+BC2=AC2,
∴AB⊥BC,
∵AB∩SA=A,
∴BC⊥面SAB;
(2)∵BC⊥面SAB,AE?面SAB,
∴BC⊥AE,
又∵AE⊥SB,SB∩BC=B,
∴AE⊥面SBC.
点评 本题主要考查了线面垂直的定义与判定定理,一般情况下,定义用来证明线线垂直,判定定理用来证明线面垂直,应注意体会线线垂直与线面垂直之间的灵活转化,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片,若从两个盒子中各随机地摸取出1张卡片,则2张卡片上的数字之积为奇数的概率为( )
| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
17.设集合A={x|(4-x)(x+3)≤0},集合B=(x|x-1<0},则(∁RA)∩B等于( )
| A. | (-∞,-3] | B. | [-4,1) | C. | (-3,1) | D. | (-∞,-3) |
1.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,点P在双曲线上,设PF1的中点在y轴上,且cos∠F1PF2=$\frac{1}{4}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
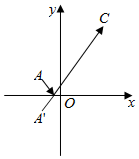 已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.