题目内容
19.甲盒子里装有分别标有数字1,2,4,7的4张卡片,乙盒子里装有分别标有数字1,4的2张卡片,若从两个盒子中各随机地摸取出1张卡片,则2张卡片上的数字之积为奇数的概率为( )| A. | $\frac{7}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
分析 先求出基本事件总数,再求出2张卡片上的数字之积为奇数包含的基本事件个数,由此能求出2张卡片上的数字之积为奇数的概率.
解答 解:甲盒子里装有分别标有数字1,2,4,7的4张卡片,
乙盒子里装有分别标有数字1,4的2张卡片,
从两个盒子中各随机地摸取出1张卡片,基本事件总数n=${C}_{4}^{1}{C}_{2}^{1}$=8,
2张卡片上的数字之积为奇数包含的基本事件个数m=${C}_{2}^{1}{C}_{1}^{1}$=2,
∴2张卡片上的数字之积为奇数的概率为p=$\frac{m}{n}$=$\frac{2}{8}=\frac{1}{4}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
9.不等式x2-2x+m>0在R上恒成立的必要不充分条件是( )
| A. | m>2 | B. | 0<m<1 | C. | m>0 | D. | m>1 |
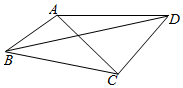 如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.
如图,在凸四边形ABCD中,AB=1,BC=$\sqrt{3}$,AC⊥CD,AC=CD,当∠ABC变化时,对角线BD的最大值为$\sqrt{6}$+1.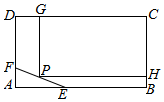 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).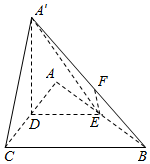 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=2a,D,E分别为AC,AB的中点,沿DE将△ADE折起,得到如图所示的四棱锥A′-BCDE,F是A′B的中点.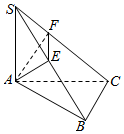 如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.
如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.