题目内容
1.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,点P在双曲线上,设PF1的中点在y轴上,且cos∠F1PF2=$\frac{1}{4}$,则双曲线的离心率为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 由PF1的中点在y轴上,可得P的横坐标为c,即有PF2⊥x轴,令x=c,可得|PF2|,再由双曲线的定义,可得|PF1|,在直角三角形PF1F2中,运用余弦函数的定义,化简可得2a2=3b2,运用a,b,c的关系和离心率公式计算即可得到所求值.
解答 解:设F1(-c,0),F2(c,0),
由PF1的中点在y轴上,可得P的横坐标为c,
即有PF2⊥x轴,令x=c,可得y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,
可得|PF1|-|PF2|=2a,即|PF1|=|PF2|+2a=$\frac{{b}^{2}}{a}$+2a,
在直角三角形PF1F2中,可得
cos∠F1PF2=$\frac{|P{F}_{2}|}{|P{F}_{1}|}$=$\frac{\frac{{b}^{2}}{a}}{\frac{{b}^{2}}{a}+2a}$=$\frac{1}{4}$,
即为2a2+b2=4b2,即3b2=3c2-3a2=2a2,
即有c2=$\frac{5}{3}$a2,可得e=$\frac{c}{a}$=$\frac{\sqrt{15}}{3}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用中点坐标公式和双曲线的定义、以及余弦函数的定义,考查化简整理的运算能力,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6.若(a-2+2ai)i为实数(其中a∈R,i为虚数单位),则|$\frac{a+i}{i}$|=( )
| A. | 5 | B. | 1 | C. | 2 | D. | $\sqrt{5}$ |
13.若a、b是方程x+lgx=4、x+10x=4的解,函数φ(x)=sin[(a+b)x+a],则函数y=φ(x)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
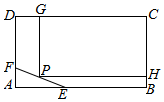 为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).
为了保护环境,实现城市绿化,某小区要在空地长方形ABCD上规划出一块长方形地面建造草坪CGPH,草坪一边落在CD上,一个顶点P在水池△AEF的边EF上,(如图,其中AB=200 m,BC=160m,AE=60m,AF=40m),设CG=xm,草坪的面积为f(x).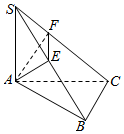 如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.
如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.