题目内容
4.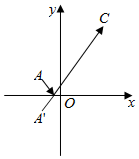 已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
已知圆C:(x-5)2+(y-7)2=4,一束光线从点A(-1,1)经x轴反射到圆周上,求光线的最短路程,并求此时的反射光线和入射光线的方程.
分析 由条件利用反射定律,直线和圆的位置关系,求得光线的最短路程,并利用两点式求此时的反射光线和入射光线的方程.
解答 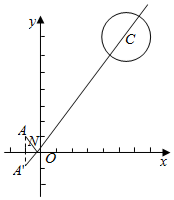 解:点A关于x轴的对称点为A′(-1,-1),光线的最短路程为A′M-2=$\sqrt{{(5+1)}^{2}{+(7+1)}^{2}}$-2=8,
解:点A关于x轴的对称点为A′(-1,-1),光线的最短路程为A′M-2=$\sqrt{{(5+1)}^{2}{+(7+1)}^{2}}$-2=8,
此时,反射光线的方程即直线A′M的方程:$\frac{y+1}{7+1}$=$\frac{x+1}{5+1}$,即 4x-3y+1=0.
故反射光线和x轴的交点为N(-$\frac{1}{4}$,0),入射光线方程即直线AN的方程:$\frac{y-0}{1-0}$=$\frac{x+\frac{1}{4}}{-1+\frac{1}{4}}$,
即4x+3y+1=0.
点评 本题主要考查反射定律,直线和圆的位置关系的应用,用两点式求直线的方程,属于中档题.

练习册系列答案
相关题目
13.若a、b是方程x+lgx=4、x+10x=4的解,函数φ(x)=sin[(a+b)x+a],则函数y=φ(x)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
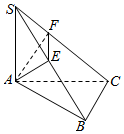 如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.
如图SA⊥面ABC,AB=3,BC=4,AC=5,AE⊥SB,求证:(1)BC⊥面SAB;(2)AE⊥面SBC.