题目内容
15．
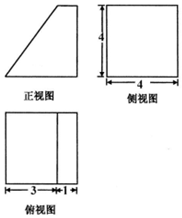某几何体的三视图如图所示（单位：cm），则该几何体的表面积是76cm2，体积是40cm3．
分析 根据几何体的三视图得该几何体是一个底面为直角梯形的四棱柱，由三视图求出几何元素的长度，由梯形的面积公式、柱体的体积公式求出该几何体的体积，由四棱柱的各个面的长度求出几何体的表面积．
解答 解：根据几何体的三视图得：该几何体是一个底面为直角梯形的四棱柱，
其底面是正视图中的直角梯形，上底为1cm，下底为4cm，高为4cm，
由侧视图知四棱柱的高为4cm，
所以该几何体的体积V=$\frac{1}{2}×（1+4）×4×4$=40（cm3），
由正视图可知直角梯形斜腰是5，
则该几何体的表面积S表面积=2×$\frac{1}{2}×（1+4）×4$+（1+4+4+5）×4=76（cm2），
故答案为：76，40．
点评 本题考查三视图求几何体的体积以及表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．一个扇形的弧长与面积的数值都是5，则这个扇形中心角的度数（ ）
| A． | 5 | B． | $\frac{5}{2}$ | C． | 3 | D． | $\frac{3}{2}$ |
6．在△ABC中，角A，B，C所对的边分别为a，b，c，若a=1，b=$\sqrt{3}$，A=$\frac{π}{6}$，则角B等于（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$或$\frac{2π}{3}$ | D． | $\frac{π}{6}$或$\frac{5π}{6}$ |
3．设函数f（x）存在导数且满足$\lim_{△x→0}\frac{f（2）-f（2-3△x）}{3△x}=2$，则曲线y=f（x）在点（2，f（2））处的切线斜率为（ ）
| A． | -1 | B． | -2 | C． | 1 | D． | 2 |
10．已知抛物线y2=4x的焦点为F，直线l过F且与抛物线交于A、B两点，若|AB|=5，则AB中点的横坐标为（ ）
| A． | $\frac{5}{2}$ | B． | 2 | C． | $\frac{3}{2}$ | D． | 1 |
7．已知长方体ABCD-A1B1C1D1中，AB=BC，AA1=2AB，E为AA1中点，则异面直线BE与CD1所形成角的余弦值为（ ）
| A． | $\frac{\sqrt{10}}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{3\sqrt{10}}{10}$ | D． | $\frac{3}{5}$ |