题目内容
4.已知$\overrightarrow{OA}$=(cos2x,-1),$\overrightarrow{OB}$=(1,sin2x+$\sqrt{3}$sin2x)(x∈R),若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$,则函数f(x)的最小值为( )| A. | -2 | B. | 0 | C. | -$\sqrt{3}$ | D. | -1 |
分析 运用向量数量积的坐标运算和二倍角的余弦公式,以及两角和的余弦公式,结合余弦函数的最值,即可得到所求最小值.
解答 解:由$\overrightarrow{OA}$=(cos2x,-1),$\overrightarrow{OB}$=(1,sin2x+$\sqrt{3}$sin2x)(x∈R),
则f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$=cos2x-sin2x-$\sqrt{3}$sin2x
=cos2x-$\sqrt{3}$sin2x
=2($\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x)
=2cos(2x+$\frac{π}{3}$),
由x∈R,可得2x+$\frac{π}{3}$=2kπ+π,即x=kπ+$\frac{π}{3}$,k∈Z时,
f(x)取得最小值-2.
故选:A.
点评 本题考查向量的数量积的坐标运算,二倍角公式和两角和的余弦公式的运用,考查余弦函数的图象和性质,主要是最值的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
19.“x≥1”是“lgx≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.如图,矩形ABCD中,AB=2,AD=1,E,F分别是BC,CD中点,则$\overrightarrow{AE}$•$\overrightarrow{AF}$=( )


| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{5}{2}$ | D. | 4 |
2.已知全集U={1,2,3,4},集合A={1,3,4},B={2,3},则A∩(∁UB)=( )
| A. | {2} | B. | {1,4} | C. | {3} | D. | {1,2,3,4} |

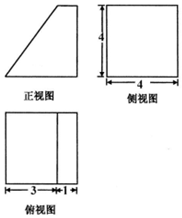 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是76cm2,体积是40cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是76cm2,体积是40cm3.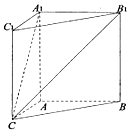 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.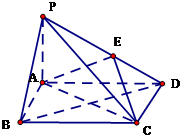 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.