题目内容
8.已知a=2${\;}^{-\frac{1}{3}}$,b=log${\;}_{\frac{1}{4}}$3,c=log25,则( )| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵a=2${\;}^{-\frac{1}{3}}$∈(0,1),b=log${\;}_{\frac{1}{4}}$3<0,c=log25>2,
则c>a>b.
故选:C.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知sin($\frac{3π}{2}$+α)=$\frac{1}{3}$,则cos(π-2α)的值等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{2}{9}$ | D. | -$\frac{2}{3}$ |
16.执行如图所示的语句,结果为( )


| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
3.已知点(2,0)到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线的距离为$\sqrt{3}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
17.“实数a、b、c不全为0“含义是( )
| A. | a、b、c均不为0 | B. | a、b、c中至少有一个为0 | ||
| C. | a、b、c中至多有一个为0 | D. | a、b、c中至少有一个不为0 |
18.若三棱锥P-ABC的三个侧面与底面ABC所成角都相等,则顶点P在底面的射影为△ABC的( )
| A. | 外心 | B. | 重心 | C. | 内心 | D. | 垂心 |
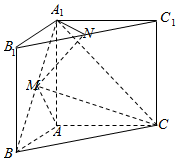 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.