题目内容
已知a1=1，a2=4，an+2=4an+1+an，bn=
，n∈N*
（Ⅰ）求b1，b2，b3的值；
（Ⅱ）设cn=bnbn+1，Sn为数列{cn}的前n项和，求证：Sn≥17n．
| an+1 |
| an |
（Ⅰ）求b1，b2，b3的值；
（Ⅱ）设cn=bnbn+1，Sn为数列{cn}的前n项和，求证：Sn≥17n．
考点：数列的求和,数列递推式
专题：综合题,点列、递归数列与数学归纳法
分析：（Ⅰ）由a1=1，a2=4，an+2=4an+1+an，可求得a3=17，a4=72，又bn=
，n∈N*，于是可求b1，b2，b3的值；
（Ⅱ）由an+2=4an+1+an，得
=4+
，即bn+1=4+
，由cn=bnbn+1，可求得c1=b1b2=17，当n≥2时，bn＞4，cn=bnbn+1=4bn+1＞17（n≥2），于是易证Sn≥17n．
| an+1 |
| an |
（Ⅱ）由an+2=4an+1+an，得
| an+2 |
| an+1 |
| an |
| an+1 |
| 1 |
| bn |
解答：
解：（Ⅰ）由于a1=1，a2=4，an+2=4an+1+an，
所以a3=4a2+a1=17，a4=4a3+a2=72，又bn=
，n∈N*，
所以b1=4，b2=
，b3=
；
（Ⅱ）证明：由an+2=4an+1+an，得
=4+
，即bn+1=4+
，
所以当n≥2时，bn＞4，
于是c1=b1b2=17，c2=b2b3=18，cn=bnbn+1=4bn+1＞17（n≥2）
所以Sn=c1+c2++cn≥17n．
所以a3=4a2+a1=17，a4=4a3+a2=72，又bn=
| an+1 |
| an |
所以b1=4，b2=
| 17 |
| 4 |
| 72 |
| 17 |
（Ⅱ）证明：由an+2=4an+1+an，得
| an+2 |
| an+1 |
| an |
| an+1 |
| 1 |
| bn |
所以当n≥2时，bn＞4，
于是c1=b1b2=17，c2=b2b3=18，cn=bnbn+1=4bn+1＞17（n≥2）
所以Sn=c1+c2++cn≥17n．
点评：本题考查数列的求和，着重考查数列递推式的应用，考查运算与求解能力，属于难题．
练习册系列答案
相关题目
若C
=C
，则n=（ ）
2n-5 11 |
n+1 11 |
| A、5 | B、6 | C、5或2 | D、5或6 |
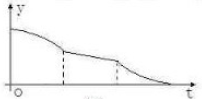
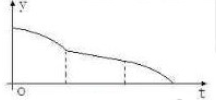
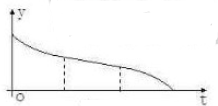
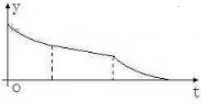
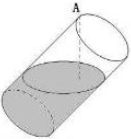一空的圆柱体容器直径小于母线长斜放，将容器斜放，使圆柱的母线与水平面成45°角，现于这种状态下由容器的最高点A处匀速地灌油，如图，则点A到油平面的距离y与灌水时间t的函数图象大致为（ ）
