题目内容
8.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C-cos2A=2sin($\frac{π}{3}$+C)•sin($\frac{π}{3}$-C).(1)求角A的值;
(2)若a=$\sqrt{3}$且b≥a,求2b-c的取值范围.
分析 (1)利用三角函数恒等变换的应用化简已知可解得:cos2A=-$\frac{1}{2}$,结合2A∈(0,2π),可得A的值.
(2)由b≥a,由(1)可得:A=$\frac{π}{3}$,又a=$\sqrt{3}$,由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}$=2,从而利用三角函数恒等变换的应用可得2b-c=2$\sqrt{3}$sin(B-$\frac{π}{6}$),结合范围B-$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{π}{2}$),可得2b-c取值范围.
解答 解:(1)∵cos2C-cos2A=2sin($\frac{π}{3}$+C)•sin($\frac{π}{3}$-C)
=2($\frac{\sqrt{3}}{2}$cosC+$\frac{1}{2}$sinC)($\frac{\sqrt{3}}{2}$cosC-$\frac{1}{2}$sinC)
=$\frac{3}{2}$cos2C-$\frac{1}{2}$sin2C
=$\frac{3}{2}$•$\frac{1+cos2C}{2}$-$\frac{1}{2}$•$\frac{1-cos2C}{2}$
=$\frac{1}{2}$+cos2C,
∴-cos2A=$\frac{1}{2}$,解得:cos2A=-$\frac{1}{2}$.
∵A∈(0,π),2A∈(0,2π),
∴当2A=$\frac{2π}{3}$时,解得:A=$\frac{π}{3}$,
当2A=$\frac{4π}{3}$时,解得:A=$\frac{2π}{3}$.
(2)∵b≥a,∴A为锐角,由(1)可得:A=$\frac{π}{3}$,
又∵a=$\sqrt{3}$,
∴由正弦定理可得:$\frac{\sqrt{3}}{sin\frac{π}{3}}$=$\frac{b}{sinB}=\frac{c}{sinC}$=2,
∴2b-c=2(2sinB-sinC)=4sinB-2sin($\frac{2π}{3}$-B)=4sinB-($\sqrt{3}$cosB+sinB)=3sinB-$\sqrt{3}$cosB=2$\sqrt{3}$sin(B-$\frac{π}{6}$),
∵B∈[$\frac{π}{3}$,$\frac{2π}{3}$),B-$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{π}{2}$),可得sin(B-$\frac{π}{6}$)∈[$\frac{1}{2}$,1),
∴2b-c=2$\sqrt{3}$sin(B-$\frac{π}{6}$)∈[$\sqrt{3}$,2$\sqrt{3}$).
点评 本题主要考查了三角函数恒等变换的应用,考查了正弦定理,正弦函数的图象和性质在解三角形中的应用,属于中档题.

| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
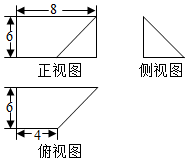 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |
| A. | (-2,3) | B. | (1,2) | C. | (2,3) | D. | (2,4) |
| A. | (2,4) | B. | [2,4] | C. | [2,4) | D. | [$\sqrt{5}$,4) |