题目内容
13.在下列条件中:①b2-4ac≥0;②ac>0;③ab<0且ac>0;④b2-4ac≥0,$\frac{b}{a}<0,\frac{c}{a}$>0中能成为“使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 根据二次方程ax2+bx+c=0的两根为正数,则一定满足b2-4ac≥0,ab<0,ac>0,故根据必要不充分条件的定义即可判断.
解答 解:∵二次方程ax2+bx+c=0的两根为正数,
∴b2-4ac≥0,ab<0,ac>0,
故由使二次方程ax2+bx+c=0的两根为正数,一定能推出b2-4ac≥0,ab<0,ac>0,
但是满足其中一个或2个不能推出使二次方程ax2+bx+c=0的两根为正数,
故①②③能成为使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件,
故选:A
点评 本题考查了一元二次方程根的情况以及充分条件和必要条件的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图P为平行四边形ABCD所在平面外一点,Q为PA的中点,O为AC与BD的交点,下面说法错误的是( ) 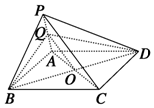

| A. | OQ∥平面PCD | B. | PC∥平面BDQ | C. | AQ∥平面PCD | D. | CD∥平面PAB |
18.函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为( )
| A. | [-$\frac{1}{2}$,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | [-$\frac{1}{2}$,$\frac{3}{4}$] | D. | (-$\frac{1}{2}$,$\frac{3}{4}$) |
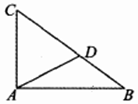 如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.
如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.