题目内容
5.已知递增等差数列{an}满足a1•a4=7,a2+a3=8.(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$,数列{bn}的前n项和为Sn,求证:Sn$<\frac{1}{2}$.
分析 (1)由题意可得公差d>0,由等差数列的性质解得a1=1,a4=7,可得公差d=2,进而得到所求通项公式;
(2)求出bn=$\frac{1}{{a}_{n}{•a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,化简整理,结合不等式的性质即可得证.
解答 解:(1)递增等差数列{an},可得公差d>0,
满足a1•a4=7,a2+a3=8,
即有a1+a4=8,
解得a1=1,a4=7,(a1=7,a4=1舍去),
可得公差d=$\frac{{a}_{4}-{a}_{1}}{4-1}$=$\frac{7-1}{3}$=2,
则数列{an}的通项公式为an=a1+(n-1)d=1+2(n-1)=2n-1;
(2)证明:bn=$\frac{1}{{a}_{n}{•a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
即有前n项和Sn=b1+b2+…+bn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)<$\frac{1}{2}$,
即为Sn$<\frac{1}{2}$.
点评 本题考查数列的通项公式的求法,注意运用等差数列的性质,考查方程思想,同时考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
| A. | $(\frac{5}{12},+∞)$ | B. | $(\frac{5}{12},\frac{3}{4}]$ | C. | $(0,\frac{5}{12})$ | D. | $(\frac{1}{3},\frac{3}{4}]$ |
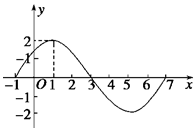 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.