题目内容
已知函数f(x)=loga
.(a>0且a≠1)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)求不等式f(x)≥loga(2x)的解.
| 3-x |
| 3+x |
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)求不等式f(x)≥loga(2x)的解.
考点:指、对数不等式的解法,奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)利用对数函数的性质确定函数的定义域.
(2)根据奇函数的定义判断即可.
(3)根据对数函数的单调性和对数的运算性质,进行分类讨论,即可
(2)根据奇函数的定义判断即可.
(3)根据对数函数的单调性和对数的运算性质,进行分类讨论,即可
解答:
解:(1)要是函数有意义,则
>0,
解得-3<x<3,
故函数f(x)的定义域为(-3,3)
(2)f(-x)=loga
=loga(
)-1=-loga
=-f(x),
所以函数f(x)为奇函数
(3)∵f(x)=loga
≥loga(2x).
当0<a<1时,
≤2x,解得x≥
,或x≤
,
∴x∈[
,3)
当a>1时,
≥2x,解得
≤x≤
,
∴x∈(-3,
]
| 3-x |
| 3+x |
解得-3<x<3,
故函数f(x)的定义域为(-3,3)
(2)f(-x)=loga
| 3+x |
| 3-x |
| 3-x |
| 3+x |
| 3-x |
| 3+x |
所以函数f(x)为奇函数
(3)∵f(x)=loga
| 3-x |
| 3+x |
当0<a<1时,
| 3-x |
| 3+x |
-7+
| ||
| 4 |
-7-
| ||
| 4 |
∴x∈[
-7+
| ||
| 4 |
当a>1时,
| 3-x |
| 3+x |
-7-
| ||
| 4 |
-7+
| ||
| 4 |
∴x∈(-3,
-7+
| ||
| 4 |
点评:本题主要考查对数函数的性质和运算及不等式的解法,要求熟练掌握对数函数的图象和性质是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若动圆与圆(x+2)2+y2=4外切且与直线x=2相切,则动圆圆心的轨迹方程是( )
| A、y2-12x+12=0 |
| B、y2+12x-12=0 |
| C、y2+8x=0 |
| D、y2-8x=0 |
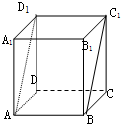 如图,正方体ABCD-A1B1C1D1中,平面ABC1D1与平面ABCD所成二面角的大小为( )
如图,正方体ABCD-A1B1C1D1中,平面ABC1D1与平面ABCD所成二面角的大小为( )| A、300 |
| B、450 |
| C、600 |
| D、900 |
已知正项等比数列{an}满足S3-3a1-2a2=0,若存在两项an•am使得
=4a1,则
+
的最小值是( )
| aman |
| 1 |
| m |
| 4 |
| n |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
 如图,在直三棱柱ABC-A1B1C1中,AA1=4,AB=5,BC=3,AC=4,D、E分半为CC1、AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=4,AB=5,BC=3,AC=4,D、E分半为CC1、AB的中点.