题目内容
5.若$\overrightarrow a=(1,\sqrt{3})$,$\overrightarrow b=(3,0)$,则$\overrightarrow a,\overrightarrow b$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
分析 利用查两个向量的数量积的定义,求得cosθ的值,可得$\overrightarrow{a}$、$\overrightarrow{b}$的夹角θ的值.
解答 解:若$\overrightarrow a=(1,\sqrt{3})$,$\overrightarrow b=(3,0)$,设$\overrightarrow a,\overrightarrow b$的夹角为θ,则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{3+0}{2•3}$=$\frac{1}{2}$,
∴θ=$\frac{π}{3}$,
故选:A.
点评 本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13.下列命题中为真命题的是( )
| A. | 命题“若x>1,则x2>1”的否命题 | B. | 命题“若x>y,则x>|y|”的逆命题 | ||
| C. | 命题“若x=1,则x2+x-2=0”的否命题 | D. | 命题“若x2≥1,则x≥1”的逆否命题 |
20.下列变量关系是函数关系的是( )
| A. | 三角形的边长与面积之间的关系 | |
| B. | 等边三角形的边长与面积之间的关系 | |
| C. | 四边形的边长与面积之间的关 | |
| D. | 菱形的边长与面积之间的关 |
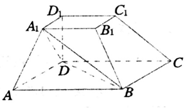 如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
如图所示,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.