题目内容
11.从甲、乙、丙三人中任选两人参加社会实践活动,甲被选中的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 从甲、乙、丙三人中任选两人参加社会实践活动,先求出基本事件总数,再用列举法求出甲被选中的基本事件个数,由此能求出甲被选中的概率.
解答 解:从甲、乙、丙三人中任选两人参加社会实践活动,
基本事件总数n=${C}_{3}^{2}$=3,
甲被选中的基本事件为{甲乙}、{甲丙},
∴甲被选中的概率p=$\frac{2}{3}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
16.在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=$\sqrt{2}$,则异面直线AB1和BC1所成角的余弦值为( )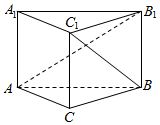

| A. | 0 | B. | $\frac{\sqrt{42}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
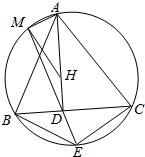 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°.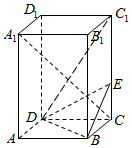 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.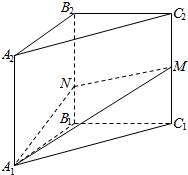 如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.
如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.