题目内容
8.函数f(x)=$\sqrt{3}$sinx•cosx的最小正周期为π,f(x)的最小值是$-\frac{{\sqrt{3}}}{2}$.分析 化简可得f(x)=$\frac{\sqrt{3}}{2}$sin2x,由周期公式可得周期,由振幅的意义可得最小值.
解答 解:化简可得f(x)=$\sqrt{3}$sinx•cosx=$\frac{\sqrt{3}}{2}$sin2x,
∴函数的最小正周期T=$\frac{2π}{2}$=π,
当sin2x=-1时,函数取最小值$-\frac{{\sqrt{3}}}{2}$.
故答案为:π;$-\frac{{\sqrt{3}}}{2}$
点评 本题考查三角函数的周期性和最值,属基础题.

练习册系列答案
相关题目
16.在正三棱柱ABC-A1B1C1中,已知AB=2,CC1=$\sqrt{2}$,则异面直线AB1和BC1所成角的余弦值为( )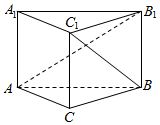

| A. | 0 | B. | $\frac{\sqrt{42}}{7}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
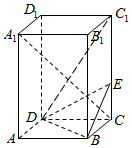 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.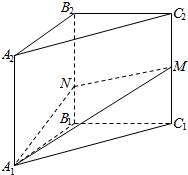 如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.
如图,在三棱柱A1B1C1-A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为$\frac{\sqrt{11}}{11}$.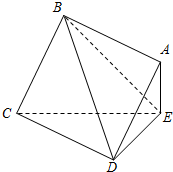 如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,
如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD, 如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为( )
如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为( )